信息安全原理与数学基础-语言识别、哥德尔不完备定理

吐槽一下，关于标题长了之后网址变得死长死长这件事

机器同余

机器同余是一个等价关系R，在有限状态机M(A,S,F)的状态集合S上的等价关系R，对于任意的s,t$\in$S，如果sRt，能导出对于任意的输入符号x$\in$A，都有F(x,s) R F(x,t)，即同一个等价类的状态对于任意的输入都转移到属于同一个等价类的状态。

有限状态机种的机器同余表现了状态之间的一种聚类性质，同一类状态经过读入字符，其目标状态还是同一类。

商机器（quotient machine)

相对于有限状态机M(A,S,F)和M上的机器同余等价关系R，S’=S/R={[s]|s$\in$S}是S关于等价关系R的商集，F’={<[s],[F(x,s)]>|s$\in$S,x$\in$A}

M’(A,S’,F’)称为M关于R的商机器M/R，通常商机器会简单一点

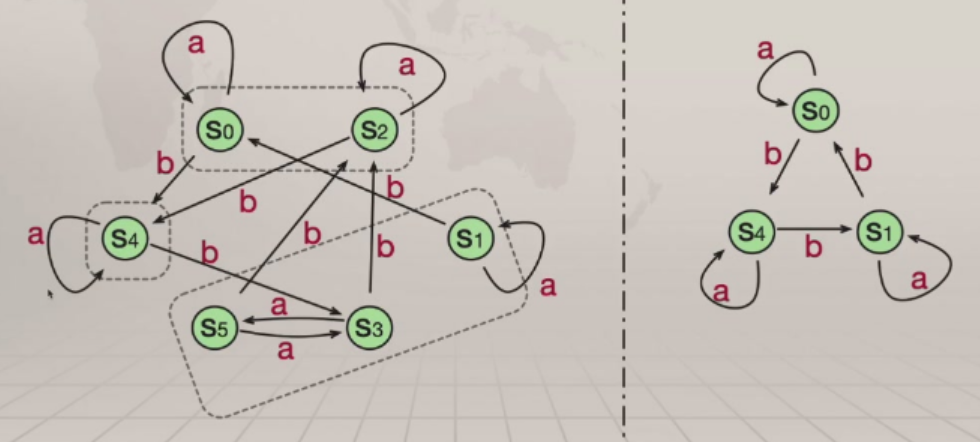
相融关系R的迭代算法

1. S的初始划分 $P_0=\{Y,Y\sim\}$
2. 假设目前已有划分$P_k=\{S_1,S_2,...,S_m\}$,考察每个等价类$S_i$
3. 如果$S_i$中的两个状态 s,t 在所有的输入x作用下都转移到同一个状态分块$A_j$(取决于x),则据此构造$S_i$的进一步细分
4. 将所有$S_i$的细分合在一起，成为新的划分$P_{k+1}$
5. 如果$P_{k+1}=P_{k}$,算法停止，否则回到第2步
6. 根据R构造商机器M/R即为化简结果

有限状态机的限制

不存在能做"操作数位数无限制"的二进制乘法的有限状态机。现实中的计算机，内存有限，能够表达的状态有限，属于一种有限状态机。

形式语言与图灵机

当W$\in$ A*，将W中的任意字符串w作为输入，M都停止在接收状态$S_Y$，而A*-W中的所有字符串，M停止在拒绝状态$S_N$，或者永不停机，则称M接受/识别语言W=L(M)。

形式语言L能被图灵机M识别，当且仅当L是一个0型形式语言。

图灵机的基本构造

一条分格的无限长的纸带，每格可容纳一个字符。一个读写头，可以在纸带上移动，读出当前格子的字符，重写格子上的内容，改变自己的内部状态。一系列关于读写头动作的规则（程序、状态、转移函数）。

状态转移函数：$\delta:Q\times\Gamma\to Q\times\Gamma\times\{L,R,N\}$

每个五元组为一条规则：$q=<s_i,a_k,s_j,a_l,d>$

• $s_i,s_j\in S$（内部状态）
• $a_k,a_l\in A$（纸带字符）
• $d\in\{L,R,N\}$（左移，右移，不动）

表示如果读写头状态为$s_i$，读到当前格子字符为$a_k$，则：

• 改写格子内容为$a_l$
• 转变状态为$s_j$
• 进行$d$指定的动作

计算规则有几条限制：规则数量有限；保证动作的确定性，任意两条规则前两项不能相同；没有规则的第一项是$S_H/S_Y/S_N$​，保证这三个状态是停机状态

识别，枚举与判定

识别：属于语言的串在有限步被接受，不属于语言的串被拒绝或者永不停机

枚举：枚举生成所有属于语言的串，对于无限集合语言，这个生成过程可能永不停止

可识别=可枚举

判定：属于语言的串被接受，且不属于语言的串被拒绝，不存在永不停机的可能

只有L和L的补语言都是图灵可识别的情况下，L才是图灵可判定的

存在语言是图灵可识别但不可判定的，和停机问题相关

哥德尔编码（Gödel Numbering）

将任何形式语言L编码为自然数的集合，将语言上的运算变换为自然数的运算，将形式系统的问题变换为数论问题。

哥德尔编码过程

定义函数$p(n)$为第n个素数，素数有无限个，且任何正整数都能唯一地写成素数的乘积

$L\subseteq A*,A=\{a_1,a_2,\cdots,a_n\}$，任意$w=a_{m_1}a_{m_2}\cdots a_{m_k}\in L$

其中$m_i$是w中第i个字符在字母表A里的序号

定义：$\displaystyle G(W)=\prod_{i=1}^kp(i)^{m_i}$​

例如$G=('accdbdd')=2^{1}\times3^{3}\times5^{3}\times7^{4}\times11^{2}\times13^{4}\times17^{4}=4677894230215956750$

所有形式语言L都是可数的

程序和通用图灵机

每个程序执行待定的计算，实现特定的功能，但我们的计算机可以执行所有程序，并得到相同的结果。通用计算机是一种特别的算法程序，将程序和程序的输入作为其输入，输出程序的输出。

每个图灵机计算特定的函数，识别特定的语言，能否有一个通用图灵机，能模拟任意图灵机的执行呢？

图灵机的编码

图灵机的定义包含有限字符集A、有限状态机S和读写头的运动规则对图灵机的描述就是一个$A\cup S\cup \{L,R,N\}$，将这个字符串进行哥德尔编码，得到图灵机的哥德尔数$G(M)$

输入、输出的编码

对图灵机的输入、输出是A上的字符串，也可以进行哥德尔编码

通用图灵机（universal Turing machine）

通用图灵机U是存在的，接受两个输入整数a,k，a是图灵机的哥德尔数，k是图灵机输入的哥德尔数

计算结果是M(a)在输入I(k)下的输出结果的哥德尔数G(o)，U所计算的函数是$U:N\times N\to N$

有趣的是，U本身也可以进行哥德尔编码，作为输入参数在U中进行计算。

停机问题

给定一个算法和相应的输入，判定这个算法是否能够完成。是否有算法能够判定某个图灵机M在输入I下是否停机，即Halt(M,I)=True if M在I处停机，Halt(M,I)=False if M在I处不停机？

答案是否定的，不存在这样的算法。停机问题是不可计算问题。

若存在这样的算法，对应图灵机Halt(a,k)，a是要判定的图灵机编码，k是输入的编码

构造TM(a):

function TM(a):
    if Halt(a,a) = False then
        return True;
    else
        loop forever

将TM编码为t，则TM(t)是一个矛盾的结果。

因此，可以得出不存在能一般性地判定图灵机停机的算法

哥德尔不完备定理

任何包含自然数定义的形式系统都是不完全的，也就是存在不能证明为真也不能证明为假的命题。

将形式系统进行哥德尔编码，将符号系统用自然数编号，所有的命题和谓词看成是符号系统上的字符串，可以得到所有命题和谓词的哥德尔数

将命题公式序列也进行编码，则$GN=2^{GN1}*3^{GN2}*5^{GN3}$，其中有三个公式。

这样：“一个序列是一个命题的证明”，我们可以写谓词R(v,x)，x是序列的哥德尔数，v是命题的哥德尔数

我们看公式：$\forall x\neg R(v,x)$表示“v不可证明”

这个谓词公式对应的哥德尔数记作GN4，考察$\forall x\neg R(GN4,x)$表示本命题不可证明。

这是一个命题，具有确定的真值，但是可否证明呢？如果可证明，那么就是证明了一个假命题，系统不一致了。如果不可证明，那么就是一个真命题，是一个定理，却不能证明，系统不完备。