机械振动
简谐振动
定义:物体运动时,离开平衡位置的位移成余弦(或正弦)规律随时间变化
x=Acos(ωt+φ)
弹簧振子运动方程
回复力:F=−kx
动力学特征:设ω2=mk,从a=mF=−mkx可得a=dt2d2x=−ω2x
二阶常微分方程:dt2d2x+ω2x=0
上述方程的解有三种形式⎩⎪⎪⎨⎪⎪⎧x=Acosωt+Bsinωtx=Acos(ωt+φ)x=Aeiωt+Be−iωt,其中ω=mk
t=0时,有x=x0,v=v0⇒x0=Acosφ,v0=−ωAsinφ,因此可以求出A与φ
振幅、周期、频率和相位
振幅(A):A=x02+(ωv0)2
周期(T):ωT=2π→T=ω2π
频率(v):单位时间内做完整简谐振动的次数,v=T1
角频率(ω):单位时间内转动的相位角
相位(ωt+φ0):初始相位φ0
相位差(Δφ):(ωt+φ2)−(ωt+φ1)=φ2−φ1=Δφ。当Δφ=±2kπ时,两振动同相位;当Δφ=±(2k+1)π时,两振动反相位。超前即Δφ>0,反之相反。
振幅矢量
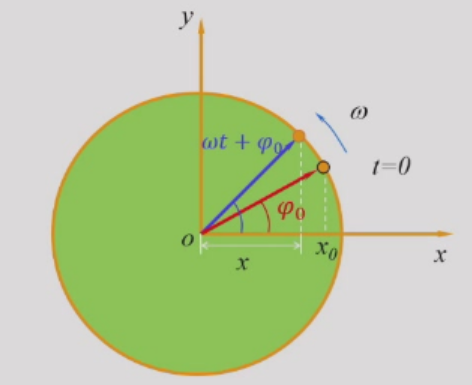
长度等于振幅A的矢量A在平面内逆时针旋转,角速度为ω。矢量在x轴上的大小就是位移x。x0对应初始位移,而φ0对应了初始振幅矢量的位置。
常见的简谐振动
单摆
小球所受合外力矩
M=−mglsinθ≈−mglθ
定轴转动定律
dt2d2θ=JM=−ml2mglθ=−lgθ
类比弹簧振子,令ω2=lg→T=ω2π=2πgl
求解方程有
dt2d2θ=−ω2θ→θ=θmcos(ωt+φ0)
物理摆
对于一个可以绕水平轴摆动的刚体构成物理摆,则J=JC+ml2,有
dt2d2θ=−Jmglθ
进一步可得ω=Jmgl
扭摆
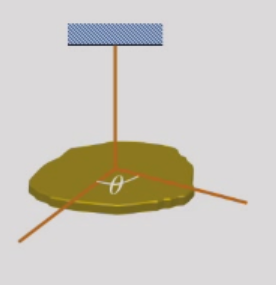
有
M=−kθM=Jdt2d2θ
可得
dt2d2θ=−Jkθ
振动的角频率为ω=Jk,扭摆的周期为T=2πkJ
简谐振动的能量
动能:Ek=21mv2=21mω2A2sin2(ωt+φ0)
势能:EP=21kx2=21kA2cos2(ωt+φ0)
系统总的机械能:(ω2=mk)
E=EK+EP=21mω2A2sin2(ωt+φ0)+21kA2cos2(ωt+φ0)
E=21kA2
简谐振动的机械能守恒,且只和振幅相关。
能量平均值
Ek=T1∫0T21mω2A2sin2(ωt+φ0)dt=41kA2Ep=T1∫0T21kA2cos2(ωt+φ0)dt=41kA2Ek=Ep=21E
简谐振动的合成
同方向同频率简谐振动的合成
若
x1=A1cos(ωt+φ1)x2=A2cos(ωt+φ2)
则合振动为
x=x1+x2=A1cos(ωt+φ1)+A2cos(ωt+φ2)
显然,合成后的振动仍然为简谐振动
从矢量图中可以求出合振幅和初相:
A=A12+A22+2A1A2cos(φ2−φ1)φ=arctanA1cosφ1+A2cosφ2A1sinφ1+A2sinφ2
若x1与x2同相,则A=A1+A2,若x1与x2反相,则A=0
同方向不同频率简谐振动的合成
若
x1=A1cos(ω1t+φ1)x2=A2cos(ω2t+φ2)
简单起见,设A1=A2=a,φ=0,则
x=2acos(2ω2−ω1)t⋅cos(2ω2+ω1)t
在∣ω2−ω1∣≪ω2+ω1时,上式中的第一项
A=2acos(2ω2−ω1)t
可看做随时间变化的振幅
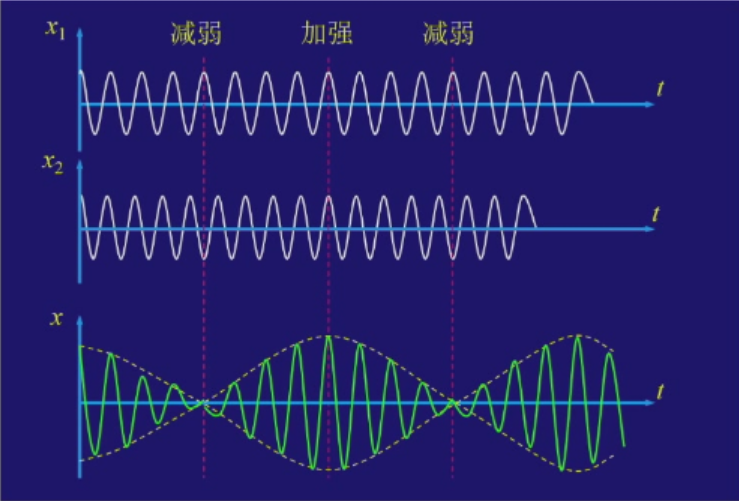
两个频率相近的简谐振动合成时,振幅作缓慢的周期性改变,称为“拍”,单位时间内振幅强弱的变化次数称为“拍频“
v拍=∣∣∣∣∣2πω2−ω1∣∣∣∣∣=∣v2−v1∣
相互垂直的简谐振动的合成
设物体同时参与两个相互垂直的振动
x=A1cos(ωt+φ1)y=A2cos(ωt+φ2)
则物体的运动轨迹应满足一椭圆方程
A12x2+A22y2−2A1A2xycos(φ2−φ1)=sin2(φ2−φ1)


