大学物理（乙）II

课堂名称：大学物理（乙）II

上课教师：陈海

通识专业通识？我不喜欢物理学（大声）

第十四章 静电场中的导体和电介质

静电场中的金属导体

导体的静电平衡

静电感应：导体置于外电场后再表面感应出电荷，形成导体内的电场平衡，即静电平衡。

导体内部场强处处为零，且整个导体是一个等式体，导体表面为等势面，表面场强处处垂直于表面。

静电平衡是导体上的电荷分布

当带电导体处于静电平衡状态是，导体内部处处没有净电荷存在，电荷只能分布在导体表面上。可用高斯定理证明（任意区域电通量为0，故没有电荷存在）。

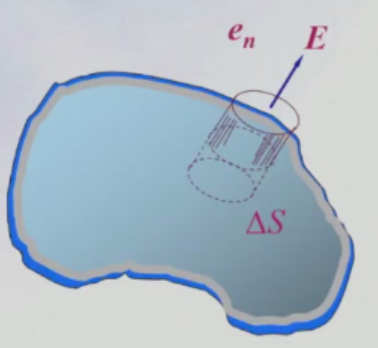
如图做高斯面，由高斯定理得：

$$\oiint\vec{E}\cdot\mathrm{d}\vec{s}=E\Delta S=\frac{\sigma\Delta S}{\varepsilon_0}$$

则$E=\frac{\sigma}{\varepsilon_0}$，写成矢量式$\vec{E}=\frac{\sigma}{\varepsilon_0}\vec{e_n}$

电荷面密度与导体表面曲率的关系

实验表明，电荷在导体表面上的分布规律与导体表面的曲率有关：曲率越大，电荷面密度越大；曲率越小，电荷面密度越小；曲率为负，电荷面密度更小。

假设将两个半径分别为R和r的球形导体用导线连接，导体组合体的电势为U。有

$$\sigma_R=\frac Q{4\pi R^2},\sigma_r=\frac q{4\pi r^2}\\ \frac{\sigma_R}{\sigma_r}=\frac{Qr^2}{qR^2}=\frac rR$$

即两球电荷面密度与曲率半径成反比，即与曲率成正比。

空腔导体内外的静电场

空腔导体在外电场中，内表面无电荷存在，导体内部及空腔内的场强等于零。

腔内电荷A可激发导体内外表面电荷，但腔内电荷A的位置不能改变导体外表面的电荷分布。导体外表面接地时，腔内电荷A不会对导体内外的物体产生影响。

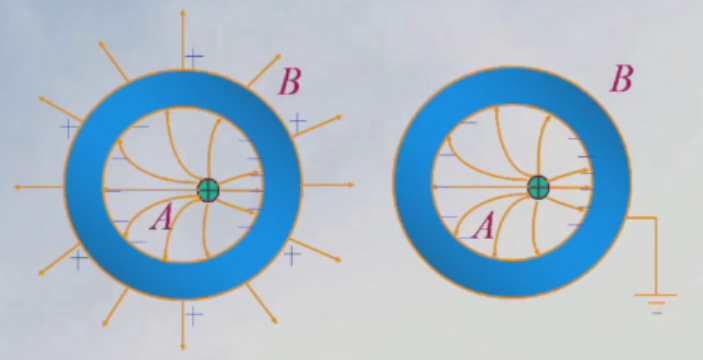
静电屏蔽

利用接地的空腔导体将腔内带电体与外界隔绝的现象。

电容 电容器

孤立导体的电容

一个鼓励导体的电势与所带电荷量呈线性关系，其比值称为孤立导体的电容

$$C=\frac qU=4\pi\varepsilon_0R,\ U=\frac 1{4\pi\varepsilon_0}\frac qR$$

电容器的电容

定义为$C=\frac Q{U_A-U_B}$

典型电容器电容的计算

平行板电容器

两极板面积S，间距d，分别带电荷+q和-q，忽略边缘效应

$$E=\frac{\sigma}{\varepsilon_0}\\ U_A-U_B=Ed=\frac{\sigma}{\varepsilon_0}d=\frac{qd}{\varepsilon_0S}\\ C=\frac{q}{U_A-U_B}=\frac{\varepsilon_0S}{d}$$

电容大小仅由材料几何结构决定。

圆柱形电容器

两同轴金属圆柱面，内外柱面半径$R_A$、$R_B$，内外柱面线电荷密度为$+\lambda$、$-\lambda$。长度无限长，忽略边缘效应。

$C=\frac{2\pi\varepsilon_0l}{\ln(R_B/R_A)}$

球形电容器

两同心金属球壳半径分别为$R_A$、$R_B$，电荷分别为+q、-q

$C=\frac q{U_A-U_B}=4\pi\varepsilon_0\frac{R_BR_A}{R_B-R_A}$

电容器的串联与并联

电容器的性能指标为电容量与耐压。多个电容器连接后，他们所带电量与两端电势差之比，成为他们的等值电容。

串联：有$\frac 1C=\frac 1{C_1}+\frac 1{C_2}+\cdots+\frac 1{C_n}$，电容减小，耐压增加

并联：有$C=C_1+C_2+\cdots+C_n$，并联增加总电容，耐压值等于其中最低的耐压值。

静电场中的电介质

电介质：电的非导体，绝缘介质。在外电场中对电场有影响，静电平衡时，内部场强不为零。

电介质对电场的影响

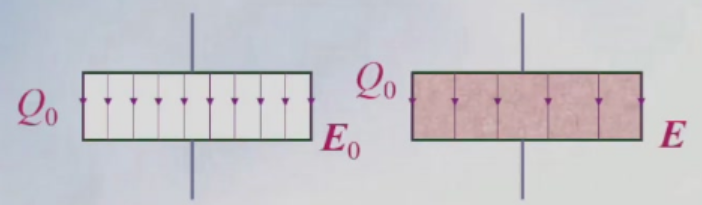
充电后$Q_0=U_0C_0$；断电后，插入电介质，电势差减小，其比例常数写为$\varepsilon_r$，称为电介质的相对介电常数，定义真空中$\varepsilon_r=1$。断电后电荷不变，电容变为原来的$\varepsilon_r$倍。场强减小$E=\frac Ud=\frac{U_0}{\varepsilon_rd}=\frac{E_0}{\varepsilon_r}$

电介质的极化

有极分子和无极分子：原子的正负电中心重合，每个原子的电偶极矩为零。几个原子构成分子时，电中心可能不重合。对有极分子，正负电荷中心组成等效分子电偶极矩p，对大量分子的等效电偶极矩之和$\sum p=0$。

电介质的极化：电介质在外场时，在于外场的垂直的表面层里出现正负电荷层，这些电荷不能自由移动，称为舒服电荷或极化电荷。这种现象称为电介质的极化。无极分子的极化称为位移极化，有极分子的极化称为取向极化。

电极化强度矢量 极化电荷面密度

单位体积内分子电偶极矩的矢量和

$$\vec{P}=\frac{\sum\vec{p}}{\Delta V}$$

称为电极化强度矢量。

实验表明，对大多数各向同性电介质：

$$\vec{P}=\chi_e\varepsilon_0\vec{E}$$

其中$\chi_e$称为介质的电极化率。

电介质中的静电场的基本定理

电介质中的场强

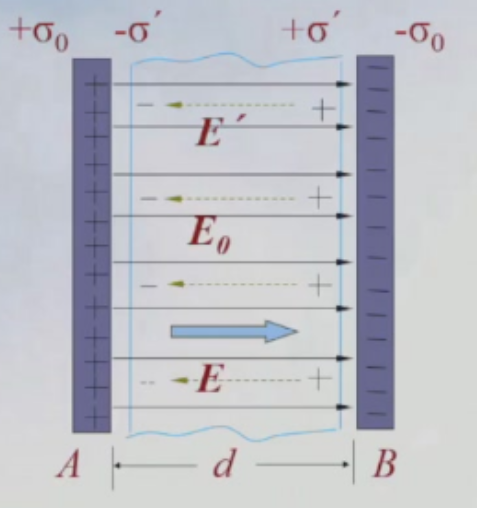
$E_0$表示自由电荷激发的电场，$E'$表示极化电荷激发的电场，介质中的合场强为$E=E_0+E'$。对充满极化率为$\chi_e$的电介质的无限大平行板电容器，设自由电荷密度为$\pm\sigma_0$，介质表面的束缚电荷密度$\pm\sigma'$，自由电荷的场强为$|E_0|=\frac{\sigma_0}{\varepsilon_0}$，舒服电荷的场强为$|E'|=\frac{\sigma'}{\varepsilon_0}$，合场强为：

$$E=E_0-E'=\frac{\sigma_0}{\varepsilon_0}-\frac{\sigma'}{\varepsilon_0}$$

将电极化强度$P$代入，有$E=\frac E{1+\chi_e}$，电介质内部的场强$E$是场强$E_0$的$\frac 1{1+\chi_e}$倍。

平行板电容器两极板间的电势差：$U=Ed=\frac{\sigma_0d}{\varepsilon_0(1+\chi_e)}$

设极板的面积为$S$，则插入电容器后，电容为原来的$\varepsilon_r$倍，由上式可知：$\varepsilon=\varepsilon_r\varepsilon_0=(1+\chi_e)\varepsilon_0$。$\varepsilon$称为介电常数或电容率。