大物乙-静电场

电荷

摩擦起电、两种电荷、电荷量、电荷力……

电荷是基本粒子的一个属性，它不能脱离这些基本粒子而存在

电荷守恒定律

在一个与外界没有电荷交换的系统内，政府电荷的代数和在任何物理过程中保持不变。

电荷守恒定律适用于一切宏观和微观过程。

电荷量子化

密立根发现带电粒子的电量只能是基本电荷e的整数倍，即粒子的电荷是量子化的。

$$q=ne\qquad n=\pm1,\pm2,\pm3\dots\\ e=1.60\times10^{-19}C$$

电荷量子化是一个实验规律，现有的实验结果表明，质子和电子的带电量差异小于$10^{-21}$

夸克模型下有分数电荷禁闭。

电荷的相对论不变性

在不同的参考系内观察，同一个带电粒子的电荷量不变。

库仑定律

点电荷

当带电体的线度与它到其他带电体的距离相比很小时，可以将其看做点电荷。

$$\vec{F_{12}}=-\vec{F_{21}}=k\frac{q_1q_2}{r_{12}^3}\vec{r_{12}}$$

系数k由实验确定，为$8.9875\times10^9(N\cdot m^2)/C^2$

引入真空电容率$\varepsilon_{0}=\frac{1}{4\pi k}=8.854187817\times10^{-12}\mathrm{C}^{2}/(\mathrm{N}\cdot\mathrm{m}^{2})$

则库仑定律可写作$\vec{F}_{12}=-\vec{F}_{21}=\frac{1}{4\pi\varepsilon_{0}}\frac{q_{1}q_{2}}{r_{12}^{3}}\vec{r}_{12}$

电场力叠加原理

处在多个点电荷作用下的电荷受力为多个点电荷作用力之和。

电场 电场强度

电场

场是某种物理量在空中的一种分布。分类有标量场、矢量场、均匀场、静场。

在物理学中，“场”是指物质的一种特殊形态。实物和场是物质的两种存在形态。它们具有不同的性质、特征和不用的运动规律。场也有质量、能量、动量和角动量。

实物是由原子分子组成的，一种实物占据的一种空间，不能同时被其他实物所占据；而场是一种弥漫在空间中的特殊物质，它遵从叠加性，即一种场占据的空间，能为其他场同时占有，互不发生影响。

标量场在空间各点只有大小，没有方向。为描述场的整体分布特征，通常采用等值面和等值线的方法，常常引入标量场的梯度。而矢量场的场值在空间不同点上既可能又不同的量值，也可能有不同的方向。为了描述场的性质，总是通过它的场线、通量和环流来进行研究。

相对于观察者静止的电荷周围所存在的场称为静电场（该电荷为场源电荷）

1. 静电场仅是电磁场的一种特殊形态。
2. 电磁场和实物物质一样具有质量、能量、动量等。
3. 电磁场一经产生就能单独存在。
4. 电磁场可在空间叠加。
5. 场和实物虽然都是物质，但又有区别。他们是物质存在的两种不同形式。
6. 两个点电荷是通过交换场量子而相互作用的，电磁场的场量子就是光子。

进入电场的任何带电体都将收到电场的作用力

电场强度

引入试探电荷$q_0$所带电量足够小，以致在电场中不会影响原有电场的分布。

定义电场强度$\vec{E}=\frac{\vec{F}}{q_0}$

电场中某点的电场强度在量值上等于放在该点的单位正试验电荷所受的电场力，其方向与正试验电荷手里方向一致。单位为(N/C)或(V/m)

点电荷与点电荷系的电场强度

点电荷的电场强度

$$\vec{E}=\frac{\vec{F}}{q_0}=\frac{1}{4\pi\varepsilon_{0}}\frac{Q}{r^{2}}\vec{r}$$

$Q>0$时，$\vec{E},\vec{r}$​同向

$Q<0$时，$\vec{E},\vec{r}$反向

点电荷系的电场强度

根据静电力的叠加原理和静电场的定义，有电场强度叠加原理$\vec{E}=\sum\vec{E_i}$

电场中任一点的总场强等于各个点电荷在该点各自产生场强的矢量和。

连续分布电荷的电场强度

任何带电体都可以看成是许多电荷元$\mathrm{d}q$的集合，在电场中任一点$P$处，每一电荷元$\mathrm{d}q$在$P$点产生的场强为：$\mathrm{d}\vec{E}=\frac{1}{4\pi\varepsilon_{0}}\frac{\mathrm{d}q}{r^{2}}\vec{r}$，整个带电体在$P$点的场强为：

$$\vec{E}=\int\mathrm{d}\vec{E}=\frac{1}{4\pi\varepsilon_{0}}\int_V\frac{\mathrm{d}q}{r^2}\vec{r}$$

实际带电体电荷连续分布的形式大致有三种

1. 体分布：$\mathrm{d}q=\rho\mathrm{d}V$​
2. 面分布：$\mathrm{d}q=\sigma\mathrm{d}s$
3. 线分布：$\mathrm{d}q=\lambda\mathrm{d}l$

电场线 电通量

电场线

曲线上任意一点的切线给出该点场强的方向一致，这一组曲线称为电场线。在电场任意一点处，通过垂直于电厂的单位截面的电场线数目正比于场强的大小。

电场线不会中断，不会相交，不会形成闭合曲线。

电通量

均匀电场中穿过与电场垂直的平面$S$的电场线总数，称为通过该平面的电场强度通量(电通量)。

$$\Phi_e=ES$$

将曲面分割为无限多个面元，称为面积元矢量$\mathrm{d}\vec{S}=\mathrm{d}S\vec{n}$，穿过该面元的电通量为$\mathrm{d}\Phi_e=\vec{E}\cdot\mathrm{d}\vec{S}=E\cos\theta\mathrm{d}S$

则穿曲面$S$的电通量为$\Phi_e=\iint_S\mathrm{d}\Phi_e=\iint E\cdot\mathrm{d}\vec{S}$

对于不闭合曲面，法线方向不唯一。对于闭合曲面，规定面元的法向矢量以穿出曲面向外为正。

高斯定理及其应用

高斯定理

在真空中，静电场通过任意闭合曲面的电通量，等于曲面内所包围的自由电荷代数和除以真空介电常数$\varepsilon_0$

$$\Phi_e=\oiint_S\vec{E}\cdot \mathrm{d}\vec{S}=\frac{1}{\varepsilon_0}\sum_iq_i\\ \Phi_e=\oiint_S\vec{E}\cdot \mathrm{d}\vec{S}=\frac1{\varepsilon_0}\int_V\rho \mathrm{d}V$$

高斯定理是电磁场的基本定理之一。对于静止电荷的电场，库仑定律和高斯定律等价。对于运动电荷的电场，库仑定律不再正确，而高斯定理仍然有效。对于牛顿引力场来说，具有与静电场相似的性质，因此只要以质量密度代替电荷密度，高斯定理在引力场中也成立。

高斯定理的应用

高斯定理普遍适用于任何静电场中，但应用高斯定理只能计算具有某种对称性分布的源电荷产生的电场，求解的关键是选取适当的高斯面。常见的具有对称性分布的源电荷有：

1. 球对称分布:包括均匀带电的球面，球体和多层同心球壳等。以均匀带电球面为例：高斯面取同心球面，显然由于高斯面与源电荷具有相同的球对称性，因此高斯面上任一点场强$E$的大小相等，方向均沿矢量$r$​，故由高斯定理：

   $$\oiint_{S_2}\vec{E}\cdot\mathrm{d}\vec{S}=\oiint_{S_2}E\cdot\mathrm{d}S=E\cdot4\pi r^2=\frac{q}{\varepsilon_0}$$

   由此求得带电球面外任一点处的场强为$\vec{E}=\frac{q}{4\pi\varepsilon_{0}r^{3}}\vec{r}$

2. 轴对称分布：包括无限长均匀带电的直线，圆柱面，圆柱体等。以无限长均匀带电圆柱面为例：高斯面取同轴封闭圆柱面，其中两底面贡献的电通量为零。
   
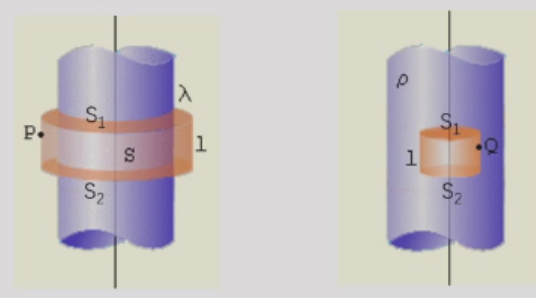
   过点$P$做长为$l$，半径为$r$的圆柱形高斯面，则电通量为：

   $$\Phi_{e}=\oint_{S}\vec{E}\cdot \mathrm{d}\vec{S}=\int_{\text{侧}}\vec{E}\cdot \mathrm{d}\vec{S}+\int_{\text{上底}}\vec{E}\cdot \mathrm{d}\vec{S}+\int_{\text{下底}}\vec{E}\cdot \mathrm{d}\vec{S}$$

   由于通过$\int_{\text{上底}}\vec{E}\cdot \mathrm{d}\vec{S}+\int_{\text{下底}}\vec{E}\cdot \mathrm{d}\vec{S}$的电通量为零，则

   $$\Phi_{e}=\oint_{S}\vec{E}\cdot \mathrm{d}\vec{S}=\int_{\text{侧}}\vec{E}\cdot \mathrm{d}\vec{S}=E\cdot2\pi rl$$

   闭合面内包围的总电荷为$\lambda l$，有高斯定理得：

   $E\cdot2\pi rl=\frac1{\varepsilon_0}\lambda l\Rightarrow E=\frac{\lambda}{2\pi\varepsilon_0r}$

3. 无限大平面电荷：包括无限大的均匀带电平面，平板等。以无限大均匀带电平面为例，高斯面取轴线垂直于带电平面、两底面对称的封闭柱面，其中侧面贡献的电通量为零。设无限大均匀带电平面的面电荷密度为$\sigma$​，通过高斯面的总电通量就是通过两底面的电通量，即：

   $$\Phi_e=\oint_S\vec{E}\cdot \mathrm{d}\vec{S}=\int_\text{侧}E\cdot \mathrm{d}\vec{S}+\int_\text{左底}E\cdot\mathrm{d}\vec{S}+\int_\text{右底}E\cdot\mathrm{d}\vec{S}\\ =ES+ES=2ES$$

   在高斯面内包围的电荷为$\sigma S$。依据高斯定理，有$2ES=\frac1{\varepsilon_0}\sigma S\Rightarrow E=\frac\sigma{2\varepsilon_0}$