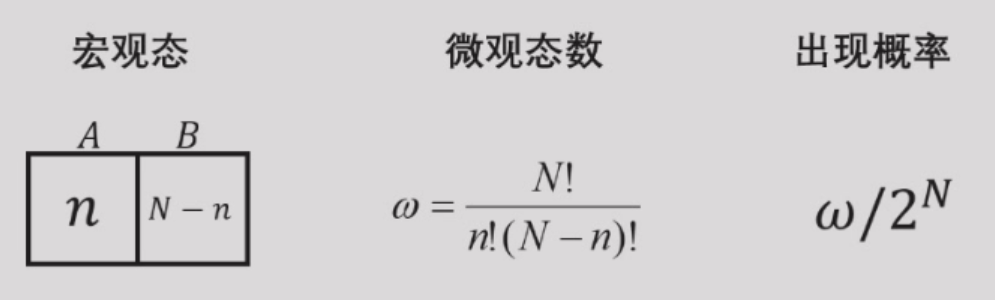大物乙-热力学基础

循环过程

循环过程

循环过程：系统经历一系列变化又回到初始状态的整个过程称为循环过程，简称循环

经过一个循环，系统的内能变化为零（$\Delta E=0$），系统吸收的净热量转化为对外做的功。

若循环的每一阶段都是准静态过程，则此循环可用$p-V$图上的一条闭合曲线表示。箭头表示过程进行的方向。

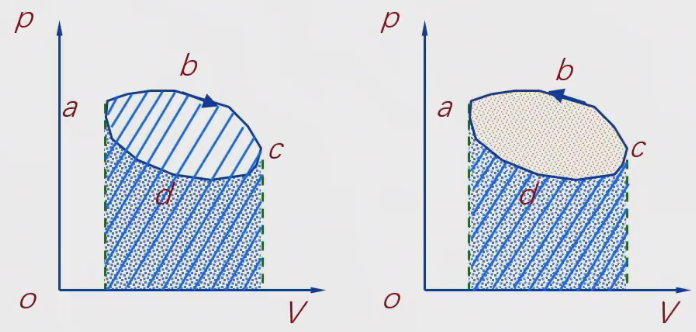
沿顺时针方向进行的循环，称为正循环或热循环。沿逆时针进行的循环称为逆循环或制冷循环。

系统膨胀对外做功>系统压缩时外界对系统做功，即热机

系统膨胀对外做功《系统压缩时外界对系统做功，即制冷机

热机的效率

热机：利用工作物质正循环将吸收的热量转变为对外做功的机器，如蒸汽机、内燃机等。

从高温热源吸热$Q_1$，对外作净功$|W|$，又向低温热源放出热量$Q_2$，而工质回到初态，内能不变。

若$Q_1,Q_2,|W|$均表示数值大小，那么工质经一循环：

$$|W|=Q_1-Q_2$$

热机效率$\eta=\frac{|W|}{Q_1}=\frac{Q_1-Q_2}{Q_1}$

制冷机及制冷系数

制冷机：利用工作物质的逆循环，不断从低温热源吸收热量，传递给高温热源的机器。

对于逆循环，工质经一循环，外界必须对系统做功$W$，系统从低温热源吸热$Q_2$，向高温热源放热$Q_1$，使低温热源温度更低，而工质回到初态，内能不变。

制冷系数$\omega=\frac{Q_2}{|W|}=\frac{Q_2}{Q_1-Q_2}$，代表了制冷机逆循环的制冷效能。

卡诺循环

卡诺循环

准静态循环，只和两个恒温热库交换热量，由两个等温过程和两个绝热过程组成。

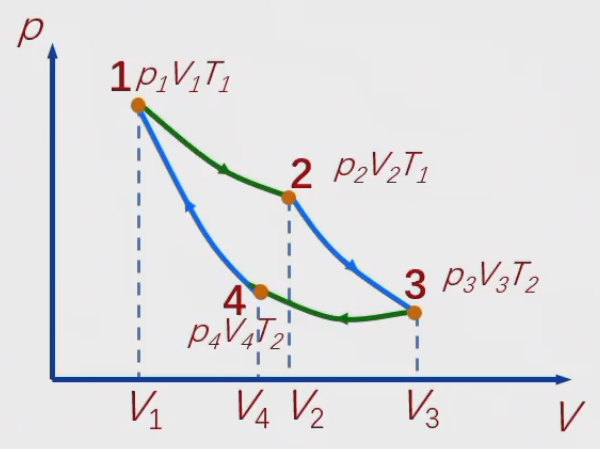
1->2

等温膨胀过程，与温度为$T_1$的高温热源接触，$T_1$不变，体积由$V_1$膨胀到$V_2$，从热源吸收的热量为

$$Q_1=vRT_1\ln\frac{V_2}{V_1}$$

2->3

绝热膨胀，体积由$V_2$变到$V_3$，吸热为零。

$$T_1V_2^{\gamma-1}=T_2V_3^{\gamma-1}$$

3->4

等温压缩，与温度为$T_2$的低温热源接触，$T-2$不变，体积由$V_3$压缩到$V_4$，对热源放热为

$$Q_2=vRT_2\ln\frac{V_3}{V_4}$$

4->1

绝热压缩，体积由$V_4$变到$V_1$，吸热为零。

$$T_1V_1^{\gamma-1}=T_2V_{4}^{\gamma-1}$$

卡诺机的效率

在一次循环中，气体对外作的净功为

$$|W|=Q_1-Q_2$$

效率为

$$\eta=\frac{|W|}{Q_1}=\frac{Q_1-Q_2}{Q_1}=1-\frac{Q_2}{Q_1}=1-\frac{T_2\ln\frac{V_3}{V_4}}{T_1\ln\frac{V_2}{V_1}}$$

根据先前$TV^{n}=c$的等式，可得$\eta=1-\frac{T_2}{T_1}$

因此，理想气体卡诺循环的效率只与两热源的温度有关。可以证明在同样两个温度$T_1$和$T_2$之间工作的各种工质的可逆热机的效率都由上式给定，而且是实际热机可能效率的最大值。

卡诺制冷机的制冷系数

在卡诺逆向循环中，工质把从低温热源吸收的热量和外界对它所作的功以热量的形式传给高温热源，其结果可使低温热源的温度更低达到制冷的目的。

在逆向卡诺机$|W|=Q_1-Q_2\quad \frac{Q_1}{Q_2}=\frac{T_1}{T_2}$

以理想气体为工质的卡诺制冷循环的制冷系数为

$$\omega_c=\frac{Q_2}{|W|}=\frac{Q_2}{Q_1-Q_2}=\frac{T_2}{T_1-T_2}$$

这是在$T_1$和$T_2$两温度间工作的各种制冷机的制冷系数的最大值。逆循环也可用做热泵，作用是将从低温热源吸取的热量提供给高温热源，如冬天的空调机。

热力学第二定律

自发过程：无需外界作用，能够自动发生的过程，其逆过程不能自动发生，但逆过程并不违反热力学第一定律。

热力学第二定律是规定自发过程方向的定律。是否存在效率为1的热机？——第二类永动机

热机的效率：$\eta=\frac{|W|}{Q_1}=\frac{Q_1-Q_2}{Q_1}$

开尔文表述：不可能从单一热源吸取热量，使之完全变成有用的功而不产生其他影响。

功可以完全变热——热不能完全变为功却不产生其他影响。存在热完全变为功的过程，例如理想气体的等温膨胀。但在这一过程中除了气体从单一热源吸热完全变为功外，还引起了其他变化，即过程结束时，气体的体积增大了。

克劳修斯表述：不可能把热量从低温物体传到高温物体，而不引起其他变化。

自然情况下，热量只能由高温物体向低温物体传递。把热量由低温物体传递到高温物体，但要以外界作功为代价，也就是引起了其他变化。

可逆过程和不可逆过程 卡诺定理

可逆过程

热力学从某状态出发，经某一过程到达另一状态，如果存在“另一过程“，它能使系统和外界完全复原，则原过程称为可逆过程。反之，称为不可逆过程。

实现可逆过程的条件：准静态过程；过程进行中无机械能损耗。

可逆过程是一种理想过程，一切与热现象有关的实际宏观过程都是不可逆的。

卡诺定理

由于卡诺循环的四个过程均满足可逆条件，故卡诺循环是可逆循环。

1. 在两个给定温度的热源之间工作的热机，不可逆热机的效率不可能大于可逆热机的效率。
2. 在两个给定温度的热源之间工作的一切可逆热机，其效率相等

$$\eta\le\frac{T_1-T_2}{T_1}$$

"=“对应可逆循环，”<"对应不可逆循环。

通过尽量提高两热源之间的温度差，或者尽量接近可逆循环，可以提高热机效率。

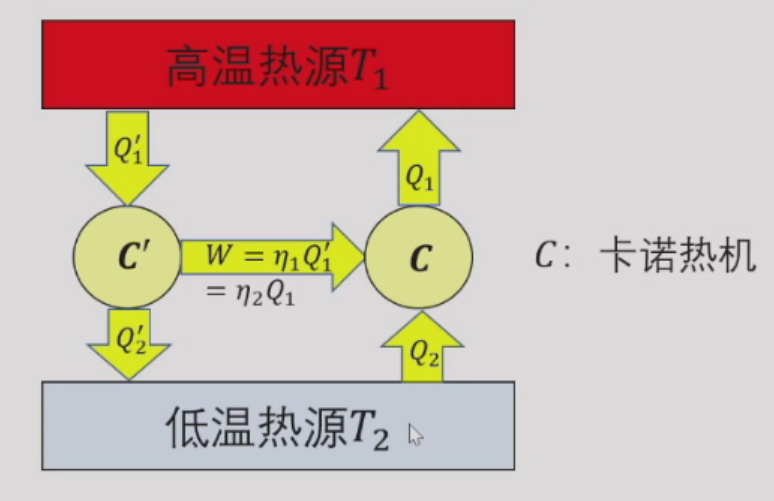
当C’为不可逆热机时，

• 若$\eta_1>\eta_2$，则$Q'_1<Q-1, Q_2'<Q_2$，整个过程违背热力学第二定律。
• 若$\eta_1=\eta_2$，则与C’不可逆的条件矛盾
• 故$\eta_1<\eta_2$

熵

1865年克劳修斯映入了状态函数熵的概念。

熵

在研究热机效率时，在卡诺循环中

$$\frac{Q_2}{Q_1}=\frac{T_2}{T_1}$$

将$Q_1$和$Q_2$用代数值来表示过程中的吸热，则上式可写成

$$\frac{Q_1}{T_1}+\frac{Q_2}{T_2}=0$$

说明在卡诺循环当中，代数值$\frac{Q}T$的总和等于零。以上结果可推广到任意可逆循环过程：

任意热循环，将其中的过程用卡诺循环代替。当卡诺循环数目趋于无限多的极限情形下，外边界折线求趋于原热循环。有

$$\oint\frac{\mathrm{d}Q}T=0$$

若将闭合曲线看成是由ABC和CDA两个可逆过程所组成，则有

$$\oint\frac{\mathrm{d}Q}T=\int_{A(B)}^C\frac{\mathrm{d}Q}T+\int_{C(D)}^A\frac{\mathrm{d}Q}T=0$$

任何可逆过程，$\frac{\mathrm{d}Q}T$的积分只决定于过程的始、末态，而与过程所经历的途径无关。

克劳修斯根据这个性质，引进一个新的态函数S，叫做熵。系统在态A时，熵为$S$，而在态$C$时，熵为$S_C$，对可逆过程：

$$\Delta S=S_C-S_A=\int_C^A\frac{\mathrm{d}Q}T$$

熵变计算

1. 熵S是态函数，与过程无关，故可自由设计可逆过程计算熵变。
2. 由于$\mathrm{d}Q$与系统的量有关，故熵具有容量性质，系统的熵变为各组成部分熵变的总和。

理想气体状态变化时熵变的计算

绝热可逆过程：

$$\mathrm{d}Q=0\quad\Delta S=\int_a^b\frac{\mathrm{d}Q}T=0$$

等体可逆过程：

$$\Delta S=\int_a^b\frac{\mathrm{d}Q_V}T=\int_{T_1}^{T-2}\frac{vC_V\mathrm{d}V}T=vC_V\ln\frac{T_2}{T_1}$$

等压可逆过程：

$$\Delta S=\int_a^b\frac{\mathrm{d}Q_p}T=\int_{T_1}^{T-2}\frac{vC_p\mathrm{d}V}T=vC_p\ln\frac{T_2}{T_1}$$

等温可逆过程：

$$\Delta S=\int_a^b\frac{\mathrm{d}Q_T}T=\frac1T(vRT\ln\frac{V_2}{V_1})=vR\ln\frac{V_2}{V_1}$$

任何可逆过程：

$$T\mathrm{d}S=\mathrm{d}Q=\mathrm{d}E+p\mathrm{d}V\\ \Delta S=vC_V\ln\frac{T_2}{T_1}+vR\ln\frac{V_2}{V_1}$$

物体可逆相变化时熵变的计算

可逆相变化是指在温度、压强和相平衡条件下的相变过程。由于温度恒定，故：

$$\Delta S=Q/T$$

T-S图上的卡诺循环

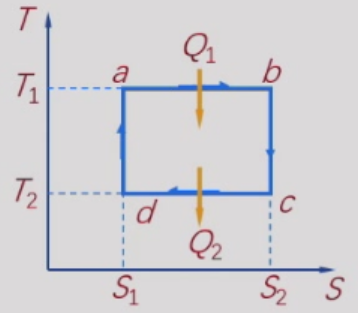
在T-S图上，卡诺循环是一矩形，由$\mathrm{d}S=\mathrm{d}Q/T$​

$$Q_1=\int_{s_1}^{s_2}T_1\mathrm{d}S=T_1(S_2-S_1)\\ Q_2=\int_{s_1}^{s_2}T_2\mathrm{d}S=T_2(S_1-S_2)\\$$

气体对外所作的净功为

$$W=Q_1-|Q_2|=(T_1-T_2)(S_2-S_1)$$

热机的效率为

$$\eta=\frac W{Q_1}=\frac{Q_1-|Q_2|}{Q_1}=\frac{T_1-T_2}{T_1}$$

熵增加原理

可以证明，对任意过程有：

$$S_B-S_A\ge\int_A^B\frac{\mathrm{d}Q}T, \mathrm{d}S\ge\frac{\mathrm{d}Q}T$$

当系统经历绝热过程时，$\mathrm{d}Q$=0，则有

$$\Delta S\ge 0$$

上式中不等号表示不可逆绝热过程，等号表示可逆绝热过程。

可逆绝热过程熵不变，不可逆绝热过程熵必然增加。孤立系统熵只增不减。

热力学第二定律的统计意义

自然过程的方向性

理想气体自由膨胀，假设容器左右等体积，左部有气体，右部为真空。抽去隔板气体自由膨胀。

• 系统宏观态：用分子在左右两部分的分配数目表示
• 系统微观态：用分子处在某一部分的具体情况表示

若有N个分子，则

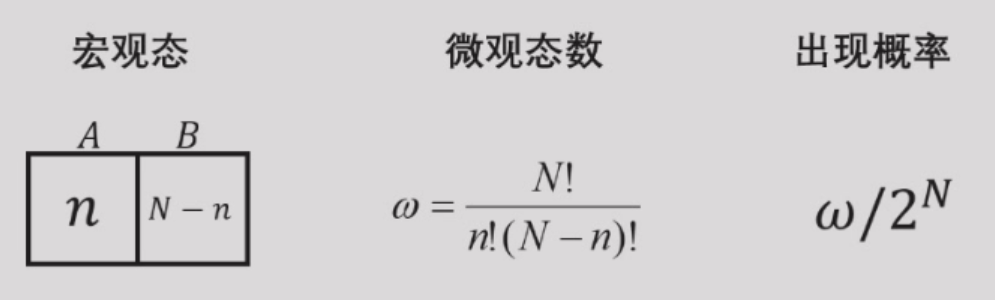
对单个分子或少量分子来说，它们扩散到右边的过程原则上是可逆的。对大量分子组成的宏观系统来说，他们向右边自由膨胀的宏观过程实际上是不可逆的。这就是宏观过程的不可逆性或自然过程的方向性在微观上的统计解释。

等概率原理和热力学概率

对于孤立系统，各种微观状态出现的可能性是相等的。各种宏观态不是等概率的。哪种宏观态包含的微观状态数多，这种宏观态出现的概率就大。

热力学第二定律的统计表述

孤立系统内部所发生的过程总是从包含微观态数少的宏观态向包含微观态数多的宏观态过渡，或者说从热力学概率小的状态向热力学概率大的状态过渡。

基于这样的考虑，玻尔兹曼提出了熵的定义

$$S=k\ln \omega$$

$$\because S_b-S_a=k\ln\frac{\omega_b}{\omega_a}>0\qquad\therefore \omega_b>\omega_a$$