大物乙-气体分子动理论

准静态过程

热力学过程：系统从一个平衡态过渡到另一个平衡态所经过的历程。
弛豫时间：旧平衡态破坏到新平衡态建立所需的时间。
准静态过程：如果热力学系统经历某一过程该过程进行得足够缓慢，且系统连续经过的每个中间态都可近似地视为平衡态，即过程经历的时间大于弛豫时间，则该过程为准静态过程。

---

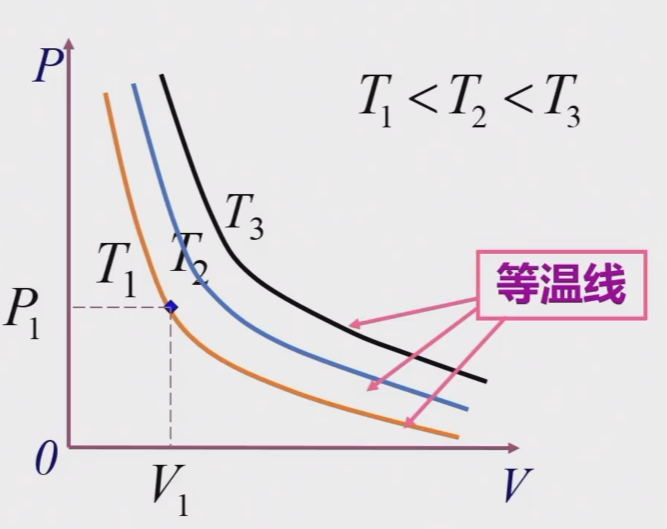
由于状态图上每一点都是平衡态，准静态过程可用$P-V$图中的一条曲线来表示。

热力学第一定律

改变热力学系统的状态可通过做功和传热，其结果使系统内能发生变化。

热力学第一定律：

$$Q=E_2-E_1+W=\Delta E+W$$

• $Q$：从外界吸热
• $W$：系统对外做功
• $E$：系统的内能

如果初、末两态无限接近，即过程为一无限小过程，则热力学第一定律可表述为：

$$\mathrm{d}Q=\mathrm{d}E+\mathrm{d}W$$

$W,Q$的正负约定

• 系统对外界做功$W>0$，系统从外界吸热$Q>0$​
• 外界对系统做功$W<0$，系统向外界放热$Q<0$

功的计算

系统对外界做元功为

$$\mathrm{d}W=F\mathrm{d}l=pS\mathrm{d}l=p\mathrm{d}V$$

$V$是系统的体积

若系统的体积由$V_1$变为$V_2$，则对外界做功

$$W=\int_{V_1}^{V_2}p\mathrm{d}V$$

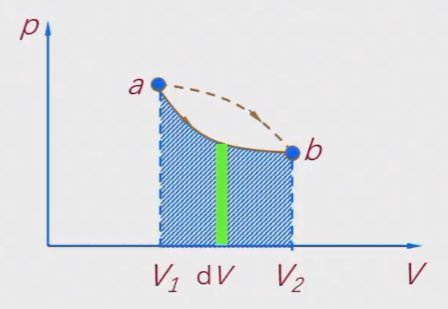
比较ab两种路径下的面积可知，功的数值不仅与初态和末态有关，而且还依赖于所经历的中间状态，功与过程的路劲有关，功是过程量。由于内能是态函数，从第一定律可知，热量也是过程量

$$Q=\Delta E+W$$

理想气体的等体过程和等压过程

一个系统温度升高$\mathrm{d}T$时，如果它吸收的热量为$\mathrm{d}Q$，则系统的热容量定义为

$$C=\mathrm{d}Q/\mathrm{d}T$$

比热$c=C/M$，摩尔热容$C_m=C/v$

因热量与过程有关，故同一系统，在不同过程中的热容量有不同的值。有实际意义的是使热传递过程在一定条件下进行，因而对应不同过程就有常用的定体热容量与定压热容量。

等体过程 定体摩尔热容

等体过程中$\mathrm{d}V=0$​，有

$$Q_r=\Delta E=v\frac i2 R\Delta T$$

系统吸收的热量全部转变为内能的增量。

定体摩尔热容为1mol物质在体积保持不变，温度升高1K所吸收的热量

$$C_V=\frac{\mathrm{d}Q_V}{v\mathrm{d}T}$$

对于理想气体$\mathrm{d}Q_V=v\frac i2R\mathrm{d}T$，则

$$C_V=\frac i2R$$

理想气体的定体摩尔热容仅与分子的自由度有关。

等体过程吸收的热量$\mathrm{d}Q_V$可表示为

$$\mathrm{d}Q_{V}=\mathrm{d}E=vC_{V}\mathrm{d}T\\ Q_{V}=\Delta E=\int_{T_{1}}^{T_{2}}vC_{V}\mathrm{d}T$$

由于内能仅为温度的函数，因而不论什么过程，只要温度的增量为$\mathrm{d}T$，内能的增量一定为

$$\mathrm{d}E=vC_V\mathrm{d}T$$

等压过程

等压过程$\mathrm{d}p=0$，功$\mathrm{d}W=p\mathrm{d}V=vR\mathrm{d}T$，内能$\mathrm{d}E=vC_V\mathrm{d}T$，有热量

$$\mathrm{d}Q=\mathrm{d}E+\mathrm{d}W=v(C_V+R)\mathrm{d}T$$

定压摩尔热容为1mol物质在压强保持不变，温度升高1K所吸收的热量

$$C_p=\frac{\mathrm{d}Q}{v\mathrm{d}T}$$

对于理想气体，有

$$C_{p}=\frac{v(C_{V}+R)\mathrm{d}T}{v\mathrm{d}T}=C_{V}+R=\frac{i+2}2R$$

1mol理想气体温度同样升高1K，等压过程将比等体过程多吸收8.31J的热量

理想气体的等温过程和绝热过程

等温过程

$\mathrm{d}T=0$，过程方程$pV=$常量，故内能$\Delta E=0$，功与热量$Q_T=W$

气体从外界吸收热量全部用来对外做功。等温过程的摩尔热容为无限大。

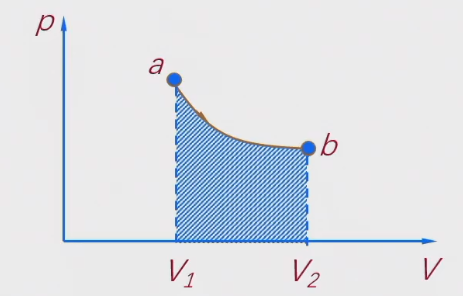
从a到b，吸收热量和对外做功为

$$Q_T=W=\int_{V_1}^{V_2}p\mathrm{d}V=\int_{V_1}^{V_2}\frac{vRT}V\mathrm{d}V=vRT\ln\frac{V_2}{V_1}$$

同样，还有$vRT\ln\frac{V_2}{V_1}=vRT\ln\frac{p_1}{p_2}$

绝热过程

系统与外界无热量交换，$\mathrm{d}Q=0$

由热力学第一定律，有$\mathrm{d}E+\mathrm{d}W=0$

绝热膨胀过程，系统对外做功，是靠内能降低实现的，故温度降低；绝热压缩过程，外界对系统做功，全部转化为内能，故温度上升。

准静态过程中气体对外界所作的功为：$\mathrm{d}W=p\mathrm{d}V$

理想气体的内能：$\mathrm{d}E=vC_V\mathrm{d}T$，式中$C_V$为定体摩尔热容量。对绝热过程有$vC_V\mathrm{d}T+p\mathrm{d}V=0$

对理想气体状态方程微分，可得：

$$vR\mathrm{d}T=p\mathrm{d}V+V\mathrm{d}p$$

两式联立，消去$\mathrm{d}T$，得到

$$(C_V+R)p\mathrm{d}V+C_VV\mathrm{d}p=0\\ \Downarrow V\mathrm{d}p+\gamma p\mathrm{d}V=0\Rightarrow\frac{\mathrm{d}p}p+\gamma\frac{\mathrm{d}V}V=0$$

其中$\gamma=\frac{C_p}{C_V}$

两边积分，得过程方程

$$pV^\gamma=c_1$$

相似的还有

$$TV^{\gamma-1}=c_2\\ p^{\gamma-1}T^{-\gamma}=c_3$$

绝热过程$\mathrm{d}Q=0$，因而摩尔热容为零。

等温线和绝热线的比较

等温方程：$pV=c\quad\frac{\mathrm{d}p}{\mathrm{d}V}=-\frac pV$

绝热方程：$pV^\gamma=c\quad\frac{\mathrm{d}p}{\mathrm{d}V}=-\gamma\frac pV$

根据泊松公式，可以画出

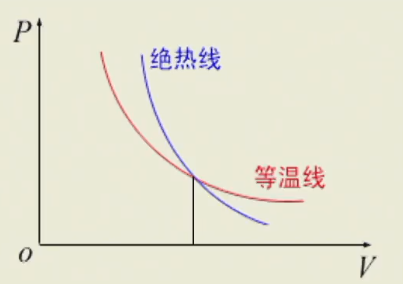
$\gamma>1$，故绝热线比等温线更陡。等温膨胀温度不变，绝热膨胀温度下降，由$p=vRT/V$可知，膨胀相同体积时，绝热过程压强降低更大。

绝热过程功的计算：借助第一定律

$$W=-\Delta E=E_1-E_2=vC_V(T_1-T_2)$$

利用泊松公式计算：

$$W=\int_{V_1}^{V_2}p\mathrm{d}V=\frac1{1-\gamma}[p_2V_2-p_1V_1]$$

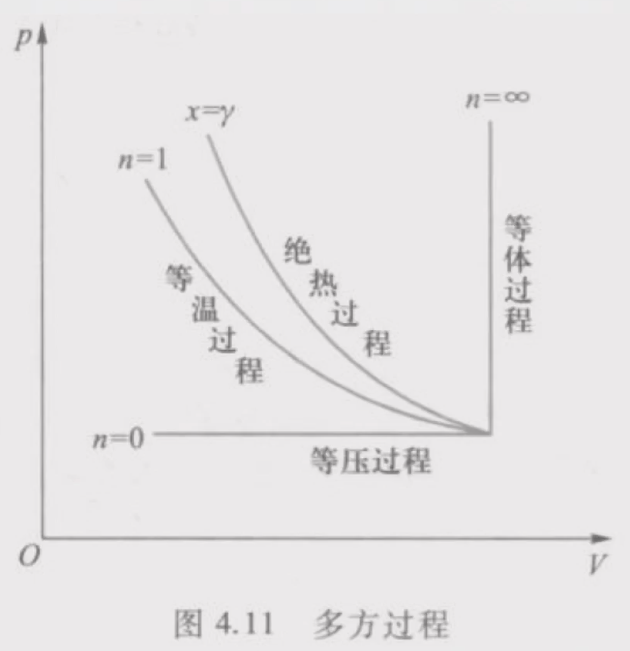
多方过程

实际上，气体所进行的过程，常常既不是等温，又不是绝热的，而是介于两者之间的，可表示为

$$pV^n=\text{常量}$$

式中n为多方指数，凡满足上式的过程称为多方过程。

• n=1：等温过程
• n=$\gamma$：绝热过程
• n=0：等压过程
• n=$\infin$：等容过程

多方过程的功：

$$W=\int_{V_1}^{V_2}p\mathrm{d}V=\int_{V_1}^{V_2}\frac{p_1V_1^n}{V^n}\mathrm{d}V=\frac1{1-n}(p_2V_2-p_1V_1)$$

可以证明，多方过程的摩尔热容

$$C_n=\frac{n-\gamma}{n-1}C_V$$

气体在多方过程中从外界吸收的热量：

$$Q=vC_n(T_2-T_1)=(vC_V-\frac{vR}{n-1})(T_2-T_1)$$

当$1<n<\gamma$时，$C_n<0$。说明气体在多方过程中对外界所做的功大于它从外界吸收的热量，多作的功是由于消耗了本身的内能，故虽然吸热，但温度反而下降，产生了负热容$Q=\Delta E+W$