大物乙-气体动理论

气体动理论利用统计方法找出热运动的宏观量（如压强、温度）与分子运动微观量的统计平均值之间的关系

热力学系统 平衡态 状态参量

热力学系统

热力学系统可分为三类：

1. 孤立系统:与外界无物质、能量交换。
2. 封闭系统:无物质交换，但有能量交换。
3. 开放系统:有物质交换，又有能量交换。

平衡态

系统宏观状态参量均匀一致，不随时间发生变化的状态。此时大量分子仍做无规则运动。有热平衡、力学平衡、化学平衡等。

热力学过程是指系统与外界交换能力，旧平衡破坏到新平衡建立的过程

状态参量

描述系统处于平衡态时的独立的宏观量

• 体积V：分子达到的空间
• 压强P：气体分子作用于器壁单位面积上的力
• 温度T：反映物理冷热程度

气体分子动理论的基本假设

分子及其运动假设

1. 分子由大量分子组成。
2. 大量分子做无规则运动叫做分子的热运动
3. 分子之间有相互作用力

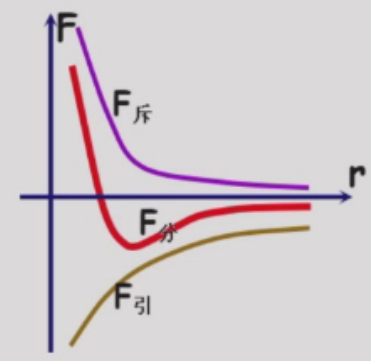
统计假设

气体处于平衡态时，分子的空间分布均匀；即气体分子的数密度处处相等

$$n=\frac{\mathrm{d}N}{\mathrm{d}V}=\frac NV$$

气体处于平衡态时，分子沿各方向运动的概率相等

$$\overline{v_x}=\overline{v_y}=\overline{v_z}=0\qquad\overline{v_x^2}=\overline{v_y^2}=\overline{v_z^2}=\frac{\overline{v^2}}3$$

理想气体的微观假设

1. 分子本身大小比起分子间距离小得多，可视为半径非常小的刚性球
2. 除碰撞的一瞬间外，分子间的相互作用力可忽略不计
3. 分子之间及分子与器壁间的碰撞是完全弹性碰撞，能量守恒

理想气体的压强公式

压强公式的导出

从微观上看，气体的压强等于大量分子在单位时间内十佳在单位面积器壁上的平均冲量

$$p=\frac{\overline{f}}S=\frac{\sum f\delta t}{dtS}$$

经过运算，可以得出压强$p=\frac13nm\overline{v^2}=\frac23n\overline{\varepsilon_k}$，其中$\overline{\varepsilon_k}=\frac12m\overline{v^2}$为分子平均动能

涨落

在一定的宏观条件下，大量分子运动的各种分布在一定的平均值附近上、下起伏变化，称为涨落现象。在任一给定瞬间或在系统中任一给定局部范围内，观测值都与统计平均值有偏差。

温度与分子平均平动动能的关系 理想气体状态方程

温度与分子平均平动动能的关系

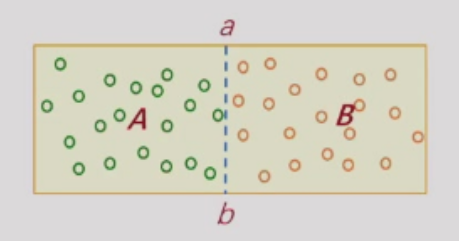
ab为导能板，接触后达到热平衡态，此时宏观物理性质称为温度。

A、B两系统达到热平衡的过程是通过导能板ab交换分子平均平动动能的结果。

态函数温度T与分子平均平动动能有单值函数关系，定义为

$$\overline{\varepsilon_t}=\frac32kT$$

温度T是分子$\overline{\varepsilon_t}$大小的量度，是一个统计关系，对个别分子无意义

上式中$k=1.38\times10^{-23}J/K$称为玻尔兹曼常数

系统整体运动的动能与温度无关。$\overline{\varepsilon_t}$是相对系统质心的。$T=t+273.15$

气体分子的方均根速率

由$\frac12m\overline{v^2}=\frac32kT$可得

$$\sqrt{\overline{v^2}}=\sqrt{\frac{3kt}m}=\sqrt{\frac{3RT}\mu}$$

$$R=N_Ak=6.02\times10^{23}\times1.38\times10^{-23}=8.31[J/(mol\cdot K)]$$

$R$称为摩尔气体常数，$N_A$为阿伏伽德罗常数，$\mu=N_Am$为气体的摩尔质量

理想气体状态方程

根据上述计算，可得$p=nkT$，由于$n=N/V,R=N_Ak$

$$pV=vRT$$

$v=\frac N{N_A}=\frac M\mu$摩尔数

能量均分原理 理想气体的内能

不同的分子具有不同的结构，理想气体分子除平动外，还有转动与振动，因此在研究分子无序运动的平均能量时，对微观模型应做适当的修正。

自由度

指决定一个物体的空间位置所需要的独立坐标数

位置需要三个自由度，转轴角度与转轴转动需要三个自由度。

• 单原子分子有三个自由度，i=3

• 双原子分子有三个平动自由度，两个转动自由度，一个振动自由度，i=6

• 刚性双原子分子，振动可忽略，i=5

• 刚性多原子分子，看成刚体，i=6

能量均分定理

$$\overline{\varepsilon_{t}}=\frac{1}{2}m\overline{v^{2}}=\frac{1}{2}m\overline{v_{x}^{2}}+\frac{1}{2}m\overline{v_{y}^{2}}+\frac{1}{2}m\overline{v_{z}^{2}}=\frac{3}{2}kT$$

在平衡态下$\overline{v_{x}^{2}}=\overline{v_{y}^{2}}=\overline{v_{z}^{2}}=\frac{1}{3}\overline{v^{2}}$，故

$$\frac{1}{2}m\overline{v_{x}^{2}}=\frac{1}{2}m\overline{v_{y}^{2}}=\frac{1}{2}m\overline{v_{z}^{2}}=\frac13(\frac{1}{2}m\overline{v^{2}})=\frac12kT$$

分子每一个平移自由度的平均动能等于$\frac12kT$

将上述结果推广到转动等其他运动形式，可得到能量均分定理：在温度为$T$的平衡态下，气体分子每个自由度的平均动能都相等，等于$\frac12kT$。若分子的自由度为i，则分子的平均动能为：

$$\overline{\varepsilon_t}=\frac i2kT$$

麦克斯韦气体分子速率分布

1859年麦克斯韦首先从理论上导出，在平衡态下理想气体分子速率分布的统计规律——麦克斯韦速率分布规律。

把速率分成很多小的区间$\Delta v$，以$\Delta N$表示$N$个分子中分布在区间$v\to v+\Delta v$中的分子数。

当$N$足够大，$\Delta v$取的充分小时，$\frac{\Delta N}{N\Delta v}$与$\Delta v,N$无关，可用来描述分子按速率的分布规律。

$$f(v)=\lim_{\Delta v\to\infty}\frac{\Delta N}{N\Delta v}=\frac{\mathrm{d}N}{N\mathrm{d}v}$$

即在速率$v$附近，单位速率区间内的分子数在总分子数中所占的比率，分布函数$f(v)$为速率$v$为连续函数。

• $f(v)\mathrm{d}v$表示在总分子$N$中，速率在$v\sim v+\mathrm{d}v$区间的分子数占分子总数的百分比。
• $Nf(v)\mathrm{d}v$表示速率在$v\sim v+\mathrm{d}v$区间内的分子数。
• $\int_{v_1}^{v_2}f(v)\mathrm{d}v$表示在总分子数$N$中，速率在$v_1\sim v_2$​区间的分子数占总分子数的百分比。
• $\int_0^\infty f(v)\mathrm{d}v$表示速率在$0\sim\infty$整个速度范围内的分子数占总分子数的比率，也就是100%，因此有$\int_0^\infty f(v)\mathrm{d}v=1$，称为$f(v)$的归一化条件。

麦克斯韦速率分布律

麦克斯韦从理论上导出理想气体在某一平衡态下的速率分布函数，即麦克斯韦速率分布函数

$$f(v)=4\pi(\frac m{2\pi kT})^\frac32e^{-\frac{mv^2}{2kT}}v^2$$

式中$m$为分子质量，$T$为温度，$k$为玻尔兹曼常数。

任一速率区间$v\sim v+\mathrm{d}v$内的分子数占总分子数的比率为

$$\frac{\mathrm{d}N}N=f(v)\mathrm{d}v=4\pi(\frac m{2\pi kT})^\frac32e^{-\frac{mv^2}{2kT}}v^2\mathrm{d}v$$

上式称为麦克斯韦速率分布律。

• $(\frac m{2\pi kT})^\frac32$为归一化因子
• $e^{-\frac{mv^2}{2kT}}=e^{-\frac{E_k}{kT}}$为玻尔兹曼因子
• $4\pi v^2\mathrm{d}v$为相空间因子

由麦克斯韦速率分布公式可求出各种统计速率：

最概然速率

气体分子的最概然速率$v_p$是速率分布函数$f(v)$取最大值的速率，即分布在$v_p$所在小区间内的分子比率最高。

令$b=\frac m{2kT}$，$f(v)=4\pi(\frac b\pi)^\frac32e^{-bv^2}v^2$

$$\begin{aligned} \frac{\mathrm{d}f}{\mathrm{d}v}\bigg|_{v=v_p}&=4\pi(\frac b\pi)^\frac32[2ve^{-bv^2}-v^22bve^{-bv^2}]_{v=v_p}\\ &=8\pi(\frac b\pi)^\frac32v_pe^{-bv^2}[1-v_p^2b]=0 \end{aligned}$$

解得$v_p=\sqrt{\frac 1b}$

由此得$v_p=\sqrt{\frac{2kt}m}=\sqrt{\frac{2RT}\mu}$​

平均速率

大量分子速率的算术平均值，称为平均速率：

$$\begin{aligned} \overline{v}&=\frac 1N\int_0^\infty v\mathrm{d}N=\frac 1N\int_0^\infty vNf(v)\mathrm{d}v=\int_0^\infty vf(v)\mathrm{d}v\\ &=4\pi(\frac m{2\pi kT})^{\frac32}\int_0^\infty e^{-\frac{mv^2}{2kT}}v^3\mathrm{d}v \end{aligned}$$

令$b=\frac m{2kT}$

$$\overline{v}=4\pi(\frac{b}{\pi})^{\frac{3}{2}}\int_{0}^{\infty}e^{-bv^{2}}v^{3}\mathrm{d}v=2\sqrt{\frac{1}{b\pi}}$$

因此有

$$\overline{v}=\sqrt{\frac{8kT}{\pi m}}=\sqrt{\frac{8RT}{\pi\mu}}$$

方均根速率

过程暂略，有结论$\sqrt{\overline{v^2}}=\sqrt{\frac{3kT}m}=\sqrt{\frac{3RT}\mu}$

可用于研究理想气体压强及分子平均平动动能等问题。$p=\frac 13 nm\overline{v^2}$

三种速率大小的比率关系：

$$v_p:\overline{v}:\sqrt{\overline{v^2}}=\sqrt2:\sqrt{\frac8\pi}:\sqrt3$$

温度T对速率分布曲线的影响

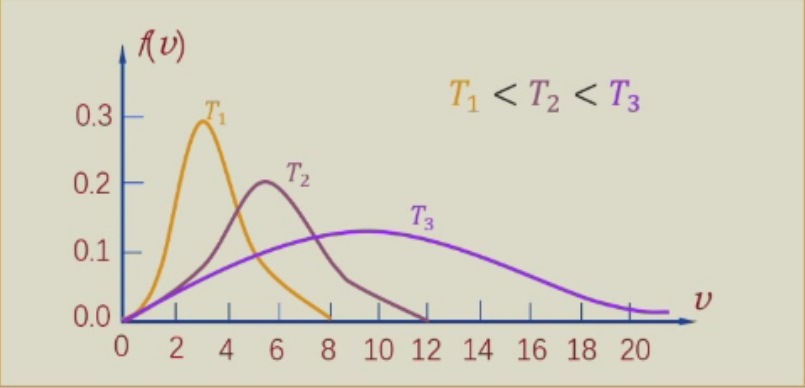
同一种理想气体在热动平衡状态下，温度升高时速率分布曲线变宽、变平坦，速率较大的分子在分子总数中的比率增大。

分子质量m对速率分布曲线的影响

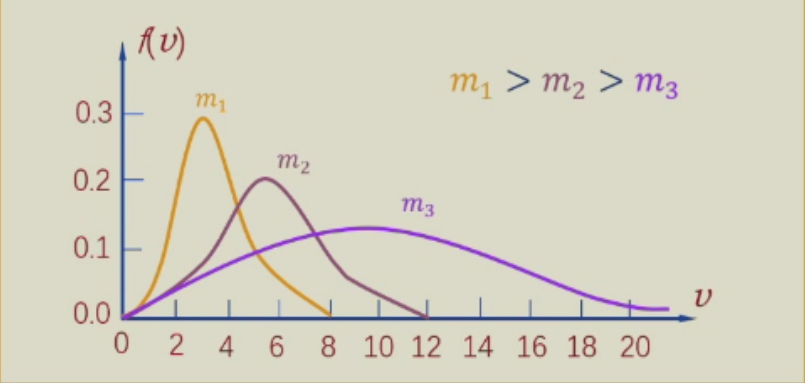
同一温度下，分子质量m越小，曲线越宽越平坦，说明在分子总数中速率较大的分子所占比率越高。

等温气压公式 玻尔兹曼分布律

等温气压公式 气体分子按势能的分布

考虑重力场中单位横截面的气柱。设$h$处压强为$p$，则$h+\mathrm{d}h$处的压强为$p+\mathrm{d}p$，则

$$\mathrm{d}p=-\rho g\mathrm{d}h$$

若气体视为理想气体，结合$\rho=nm=\frac p{kT}m=\frac{pu}{RT}$，有：

$$\frac{\mathrm{d}p}p=-\frac{\mu g}{RT}\mathrm{d}h$$

设$g$与$T$均匀，则有等温气压公式：

$$p=p_0e^{-\frac{\mu gh}{RT}}$$

式中$p_0$为$h=0$处的压强。

将$p=nkT$代入，分子密度按高度的分布为：

$$n=\frac{p_0}{kT}e^{-\frac{\mu gh}{RT}}=n_0e^{-\frac{\mu gh}{RT}}=n_0e^{-\frac{\varepsilon_p}{RT}}$$

$n$为高度为$h$处的分子数密度，$n_0$为$h=0$处的数密度，$\varepsilon_p$为分子的重力势能。

玻尔兹曼分布

在麦克斯韦速率分布中，有一因子：

$$e^{-mv^{2}/2kT}=e^{-\varepsilon_{k}/kT}$$

假如气体分子有势能$\varepsilon_p=\varepsilon_p(x,y,z)$

气体分子有总能量$\varepsilon=\varepsilon_p+\varepsilon_k$

玻尔兹曼推广：气体分子速度在区间$v_x\sim v_x+\mathrm{d}v_x\qquad v_y\sim v_y+\mathrm{d}v_y\qquad v_z\sim v_z+\mathrm{d}v_z$；位置在$x\sim x+\mathrm{d}x\qquad y\sim y+\mathrm{d}y\qquad z\sim z+\mathrm{d}z$的分子数目为：

$$\mathrm{d}N_{v,r}=n_0(\frac m{2\pi kT})^{\frac 32}e^{-\frac{\varepsilon}{kT}}\mathrm{d}v_x\mathrm{d}v_y\mathrm{d}v_z\mathrm{d}x\mathrm{d}y\mathrm{d}z$$

$n_0$为$\varepsilon_p=0$时的分子数密度

$e^{-\frac{\varepsilon}{kT}}$称为玻尔兹曼因子。玻尔兹曼统计：温度$T$的平衡状态下，某一状态区间的粒子数与该状态区间的例子的能量$\varepsilon$有关，而且与$e^{-\frac{\varepsilon}{kT}}$成正比。

上式对所有可能的速度积分，即得数密度按高度分布公式

$$n=n_0e^{-\frac{\varepsilon_p}{kT}}$$

$$\mathrm{d}N'=\cdots=n_0e^{-\frac{\varepsilon_p}{kT}}\mathrm{d}x\mathrm{d}y\mathrm{d}z$$

能量量子化与玻尔兹曼分布

粒子只能分布在一系列不连续的能量值上，称为能级。

设系统有$N$个分子，对应能级$\varepsilon_0\sim N_0$，则当$N,V,U\text{(内能)}$一定时，分子按能量分布为：

$$N_i=Ae^{-\varepsilon_i/kT}$$

其中$A$与$N,V,T$有关

气体分子的平均自由程

分子碰撞模型

在研究分子碰撞规律时，可把气体分子看做无吸引力，有效直径为$d$的刚性球。

由于碰撞，气体分子运动的径迹是一条迂回曲折的路线，每个分子在任意两次碰撞之间所行自由路程的张端、所经历的时间都是随机的。

平均自由程：在一定的条件下，一个气体分子在连续两次碰撞之间可能通过的各段自由程的平均值，记为$\overline{\lambda}$​

平均自由程的计算

平均碰撞频率$\overline{Z}$：一个分子单位时间内与其他分子的平均碰撞次数。

设分子A以平均速率$\overline{v}$运动，其它分子静止。容易得到

$$\overline{\lambda}=\frac{\overline{v}\cdot\Delta t}{\overline{Z}\cdot\Delta t}==\frac{\overline{v}}{\overline{Z}}$$

运动方向上，以$d$为半径的圆柱体内的分子都将与分子A碰撞，碰撞截面$\sigma=\pi d^2$

单位时间内分子A走$\overline{v}$，相应圆柱体体积为$\overline{v}\sigma$

则$\overline{Z}=n\overline{v}\sigma$

考虑到其他分子都在运动，平均速率改为相对平均速率，故$\overline{Z}=\sqrt{2}n\overline{v}\sigma$

平均自由程：

$$\overline{\lambda}=\frac{\overline{v}}{\overline{Z}}=\frac{1}{\sqrt{2}\pi d^{2}n}=\frac{kT}{\sqrt{2}\pi d^{2}p}$$

标准状态下$\overline{Z}\sim6.5\times10^9\mathrm{s}^{-1},\bar{\lambda}\sim6.9\times10^{-8}\mathrm{m}$

特例：如果气体容器线度小于平均自由程计算值时，实际平均自由程就是容器线度的大小。