.
- 能用重积分解决的实际问题的特点
- 所求量是分布在有界闭域上的整体量
- 所求量对区域具有可加性
- 用重积分解决问题的方法:用微元分析法建立积分式
立体体积
曲顶柱体的顶为连续曲面z=f(x,y),(x,y)∈D,则其体积为
V=∬Df(x,y)dxdy
占有空间有界域Ω的立体的体积为
V=∭Ddxdydz
例1
求曲面S1:z=x2+y2+1 任一点的切平面与曲面S2:z=x2+y2所围立体的体积 V
解:
曲面S1在点(x0,y0,z0)的切平面的方程为
z=2x0x+2y0y+1−x02−y02
与曲面z=x2+y2的交线在xOy面上投影为
(x−x0)2+(y−y0)2=1
∴V=∬D[2x0x+2y0y+1−x02−y02−x2−y2]dxdy=[1−((x−x0)2+(y−y0)2)]dxdy↓令x−x0=rcosθ,y−y0=rsinθ=π−∬Dr2⋅rdrdθ=π−∫02πdθ∫01r3dr=2π
曲面的面积
设光滑曲面S:z=f(x,y),(x,y)∈D,则面积A可看成曲面上各点M(x,y,z)处小切面的面积dA无限积累而成,设它在D上的投影为dσ,则
dσ=cosγ⋅dA↓cosγ=1+fx2(x,y)+fy2(x,y)1dA=1+fx2(x,y)+fy2(x,y)dσ
故有曲面公式
A=∬D1+(∂x∂z)2+(∂y∂z)2dxdy
例2
计算双曲抛物面z=xy被柱面x2+y2=R2所截出的面积A
解:
曲面在xOy上的投影为D:x2+y2≤R2,则
A=∬D1+zx2+zy2dxdy=∬D1+x2+y2dxdy=∫02πdθ∫0R1+r2rdr=32π[(1+R2)23−1)]
例3
计算半径为a的球的表面积
解:
利用球坐标方程,设球面方程为r=a,球面面积元素为dA=a2sinφdφdθ
∴A=a2∫02πdθ∫0πsinφdφ=4πa2
物体的质心
设空间有n个质点,分别位于(xk,yk,zk),其质量分别为mk,由力学知,该质点系的质心坐标为
x=∑k=1nmk∑k=1nxkmky=∑k=1nmk∑k=1nykmkz=∑k=1nmk∑k=1nzkmk
将Ω分成n小块,任取一点(ξk,ηk,ζk),有
x≈∑k=1nρ(ξk,ηk,ζk)Δvk∑k=1nξkρ(ξk,ηk,ζk)Δvk
令区域直径λ→0,即得
x=∭Ωρ(x,y,z)dxdydz∭Ωxρ(x,y,z)dxdydz
当ρ(x,y,z)≡常数时,则得形心坐标
x=V∭Ωxdxdydz
例4
求位于两圆r=2sinθ和r=4sinθ之间均匀薄片的质心
解:
利用对称性可知x=0
而
y=A1∬Dydxdy=3π1∬Dr2sinθdrdθ=3π1∫0πsinθdθ∫2sinθ4sinθr2dr=9π56∫0πsin4θdθ=9π56⋅2∫0π/2sin4θdθ=9π56⋅2⋅43⋅21⋅2π=37
物体的转动惯量
对z轴的转动惯量为
dIz=(x2+y2)ρ(x,y,z)dv
因此物体对z轴的转动惯量为
Iz=∭Ω(x2+y2)ρ(x,y,z)dxdydz
对于另外两轴类似,对于原点转动惯量为
IO=∭Ω(x2+y2+z2)ρ(x,y,z)dxdydz
例5
求半径为a的均匀半圆薄片对其直径的转动惯量
解:
建立坐标系如图
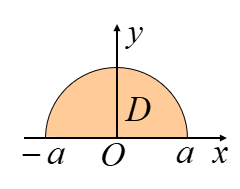
∴Ix=∬Dμy2dxdy=μ∬Dr3sin2θdrdθ=μ∫0πsin2θdθ∫0ar3dr=41μa4⋅2⋅21⋅2π=41Ma2
物体的引力
dFx=Gr3ρ(x,y,z)(x−x0)dv
引力分量为
Fx=G∭Ωr3ρ(x,y,z)(x−x0)dv
其中r=(x−x0)2+(y−y0)2+(z−z0)2
例6
设面密度为μ,半径为R的圆形薄片x2+y2≤R2,求它对位于点M0(0,0,a)处的单位质量质点的引力
解:
由对称性知引力F=(0,0,Fz)
dFz=Gd3μ(0−a)dσ=−Gaμ(x2+y2+a2)3/2dσ
∴Fz=−Gaμ∬D(x2+y2+a2)3/2dσ=−Gaμ∫02πdθ∫0R(r2+a2)3/2rdr=2πGaμ(R2+a21−a1)
