大物乙-机械振动II

机械波动

机械波

机械波的形成

机械波是机械振动在介质中的传播。

机械波的形成条件：波源、弹性介质。

横波与纵波

横波：振动方向与传播方向垂直的波

纵波：振动方向与传播方向平行的波

波面与波线

波面：振动相位相同的各点组成的面

波前：任意时刻波所到达的最前面的波面

波线：波的传播方向，用带箭头的线表示

波速：单位时间，某一确定相位传播的距离

惠更斯原理

波面上每一点都可看作是发射子波的波源，这些子波的包迹就是新波面。传播过程中经过障碍物，偏离直线传播的现象称为衍射。

平面简谐波

定义

在平面内作机械振动的波。

一维简谐波的一般表达式

$$y_0(t)=A\cos(\omega t+\varphi_0)\\ y(x=0,t)=A\cos(\omega t+\varphi_0)$$

该振动以速度$u$沿x轴向正向传播

从x=0点传播到x点处所需时间：x/u

$$y(x,t)=A\cos\omega(t-\frac xu)$$

落后相位即为$\omega\frac xu$。此式即为简谐波的波函数，或波动方程。

当$t=t_0$给定，波动方程为$f(x,t_0)=A\cos\omega(t_0-\frac xu)$，上式反映了$t=t_0$时刻的波形图，途中相位差为$2\pi$的两点之间的距离为波长。由方程可得

$$\omega(t_0-\frac xu)-\omega(t_0-\frac{x+\lambda}u)=\omega\frac\lambda u=2\pi$$

波的周期定义为$T=\frac \lambda u=\frac {2\pi}\omega$

波的频率定义为单位时间内沿波线所推进的完整波的数目$v=\frac u\lambda=\frac \omega{2\pi}$​

因此波的频率和周期由波源决定

当$x=x_0$给定，波动方程为$y(x_0,t)=A\cos\omega(t-\frac{x_0}u)$，方程反映的是点$x=x_0$的振动方程。

波的能量 能流密度

波的能量

弹性波传播到介质某处，该点由不动到动，因而具有动能；该处介质将产生形变，因而具有势能。介质由近及远的振动，相应能量向外传播。以一维纵波在棒中传播为例：

在棒中任取体元$\Delta V$、质量为$\Delta m=\rho\Delta V$。波传播到此体元时，体元具有动能$W_k$和势能$W_p$。 设$y(x,t)=A\cos\omega(t-\frac xu)$。当动能达到最大时势能也最大，这与简谐振子完全不同。因为波在介质中传播时，与势能相关的是质点间的相对位移$\Delta y/\Delta x$

$$v=\frac{\partial y}{\partial t}=-A\omega\sin\omega(t-\frac xu)\\ W_k=\frac12(\Delta m)v^2=\frac12\rho(\Delta V)v^2\\ W_k=W_p=\frac12\rho A^2\omega^2(\Delta V)\sin^2\omega(t-\frac xu)$$

体元的总机械能

$$W=W_k+W_p=\rho A^2\omega^2(\Delta V)\sin^2\omega(t-\frac xu)$$

波的能量密度：介质中波的单位体积的能力称为能量密度

$$w=\rho A^2\omega^2\sin^2\omega(t-\frac xu)$$

平均能量密度：能量密度在一个周期内的平均值

$$\overline{w}=\frac1T\int_0^Tw\mathrm{d}t=\frac1T\int_0^T\rho A^2\omega^2\sin^2\omega(t-\frac xu)\mathrm{d}t=\frac12\rho A^2\omega^2$$

机械波的能量与振幅、频率的平方成正比，这对弹性介质上传播的各种简谐波均成立。

平均能流密度（波的强度）：单位时间内通过垂直于波传播方向单位面积的能量的时间平均值

$$I=\overline{w}u=\frac12\rho A^2\omega^2u$$

对于平面波：$y=A\cos\omega(t-\frac xu)$平面波通过1、2两平面平均能流分别为

$$\overline{P_1}=\overline{w_1}uS=\frac12\rho A_1^2\omega^2uS\qquad\overline{P_2}=\overline{w_2}uS=\frac12\rho A_2^2\omega^2uS$$

对于无吸收介质，通过两平面的总能流相等

$$\overline{P_1}=\overline{P_1}\qquad A_1=A_2$$

平面波在无吸收介质中传播满足振幅不变条件。

对于球面波：波源到$r_1$、$r_2$两球面，面积分别为$S_1=4\pi r_1^2$和$S_2=4\pi r_2^2$

对无吸收介质，通过两球面的总能流相等：

$$\frac12\rho A_1^2\omega^2u4\pi r_1^2=\frac12\rho A_2^2\omega^2u4\pi r_2^2$$

由上式得：$A_1r_1=A_2r_2$，即振幅和离开波源的距离成反比，故球面波的表达式为$y(r,t)=\frac{A_0}r\cos\omega(t-\frac xu)$，式中$A_0$为波离波源单位距离处的振幅。

叠加原理 波的干涉

叠加原理

几列波相遇后，每列波都保持原有的特性（频率、振幅、波长、振动方向等），这几列波在相遇区质点的振动是各列波所引起的振动的合成。这一规律为波传播的独立性或可叠加性。

波的干涉

几列波在相遇空间叠加后的强度，在某些地方始终加强，而在另一些地方始终减弱的现象，称为波的干涉。

• 两列波的振动频率相同
• 振动方向相同
• 振动相位有恒定的相位差

对于

$$y_{1}=A_{1}\cos(\omega t-\frac{2\pi}{\lambda}r_{1}+\varphi_{1})\\y_{2}=A_{2}\cos(\omega t-\frac{2\pi}{\lambda}r_{2}+\varphi_{2})$$

合成后的方程为

$$y=y_1+y_2=A\cos(\omega t+\varphi)$$

其中

$$A=\sqrt{A_{1}^{2}+A_{2}^{2}+2A_{1}A_{2}\cos\Delta\varphi}\\\Delta\varphi=(\varphi_{2}-\varphi_{1})-\frac{2\pi}{\lambda}(r_{2}-r_{1})$$

当$\Delta\varphi=\pm2k\pi$时，$A=A_{max}=A_1+A_2$，强度$I=I_{max}=I_1+I_2+2\sqrt{I_1I_2}$。此时称为干涉相长

当$\Delta\varphi=\pm(2k+1)\pi$时，$A=A_{min}=|A_1-A_2|$，强度$I=I_{min}=I_1+I_2-2\sqrt{I_1I_2}$。此时称为干涉相消。

当$\varphi_1=\varphi_2$时，$\Delta\varphi$完全取决于波程差$\delta=r_2-r_1\quad\Delta\varphi=-\frac{2\pi}\lambda\delta$

当$\delta=r_2-r_1=\pm k\lambda$​时,对应干涉相长

当$\delta=r_2-r_1=\pm (2k+1)\frac\lambda2$时,对应干涉相消。

驻波

两列相向运动的等振幅相干波叠加式形成驻波。

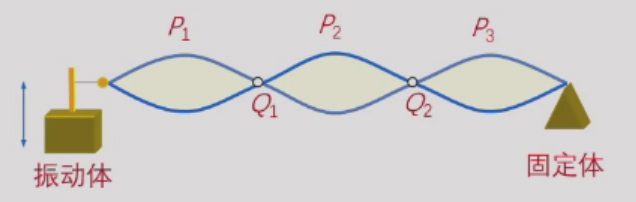
在所形成的驻波中$Q_1\ Q_2$称为波节，$P_1\ P_2\ P_3$​称为波腹。

驻波的表达式

设两列在x方向相向传播的波，波函数的表达式为

$$y_{1}=A\cos(\omega t-\frac{2\pi}{\lambda}x)\quad y_{2}=A\cos(\omega t+\frac{2\pi}{\lambda}x)$$

按照叠加原理最终可以得到

$$y=2A\cos\frac{2\pi}\lambda x\cos\omega t$$

上式$\cos\omega t$表示谐振动，$\left|2A\cos\frac{2\pi}{\lambda}x\right|$表示谐振动的振幅。

从能量角度看，对于行波，随着波的传播，也伴随着能量的不断传播。用平均能流密度表示。对于驻波，两波的平均能流密度为$\overline{w}u$和$-\overline{w}u$。即大小相等，方向相反，总能量为0，介质的动能和势能不断相互转换。

通过计算，动能最大值出现的位置为波腹，而势能最大值出现的位置为波节。

驻波的特点

相邻两波节之间各质点相位相同；波节两侧各质点相位相反。驻波不是振动状态的传播，也没有能量的传播。

半波损失

当波从一种介质垂直入射到第二种介质时，如果第二种介质的密度与波速的乘积远大于第一种介质的密度与波速的乘积（前者称为波密介质，后者称为波疏介质），即$\rho_2u_2\gg\rho_1u_1$，则分界面处将出现波节，这时入射波与反射波在分界面有$\pi$的相位突变，从波长的角度考虑有$\lambda$的波长差，此现象称为半波损失。

多普勒效应 激波

多普勒效应

波源与观察者之间有相对运动时，观察者接受到的波的频率$v_R$与波源的振动频率$v_S$不同，这种现象称为多普勒效应。

设波源和观察者的运动在两者的连线上，设波源运动速度$v_S$，观察者运动速度$v_R$。

1. 波源和观察者都不运动：$v_S=0,v_R=0$，有$\nu_R=\frac u\lambda=\nu_S$
2. 波源不动，观察者以速度$v_R$相对波源运动：$\nu_R=\frac{u+v_R}\lambda=\frac{u+v_R}{uT_S}=(\frac{u+v_R}u)\nu_S$。或者远离波时$\nu_R=(\frac{u-v_R}u)\nu_S$
3. 观察者不动，波源以速度$v_S$向观察者运动：媒质中的波长为$\lambda'=\lambda-v_ST_S=(u-v_S)T_S$，因此波的频率 $\nu_R=\frac{u}{\lambda'}=\frac u{(u-v_S)T_S}=\frac u{u-v_S}\nu_S$。当波源远离观察者时$\nu_R=\frac{u}{u+v_S}\nu_S$
4. 两者都运动时：$\nu_R=\frac{u\pm v_R}{\lambda\mp v_ST_S}=\frac{u\pm v_R}{u\mp v_S}\nu_S$