关于我睡过头这节微积分课完全没听这件事,后来补的笔记
三重积分的概念
引例
设在空间有限闭区域Ω内分布着某种不均匀的物质,密度函数为μ(x,y,z)∈C,求分布在Ω内的物质的质量M。类似二重积分的思想,可得
M=λ→0limk=1∑nμ(ξk,ηk,ζk)Δvk
设f(x,y,z),(x,y,z)∈Ω,若对Ω作任意分割:Δvk,任意取点(ξk,ηk,ζk)∈Δvk,下列乘积和式极限
λ→0limk=1∑nf(ξk,ηk,ζk)Δvk记作∭Ωf(x,y,z)dv
存在,则称此极限为函数f(x,y,z)在Ω上的三重积分。
三重积分的性质与二重积分相似,例如中值定理:设f(x,y,z)在有界闭域Ω上连续,V为Ω的体积,则存在(ξ,η,ζ)∈Ω使得
∭Ωf(x,y,z)dv=f(ξ,η,ζ)V
三重积分的计算
利用直角坐标计算三重积分
先假设连续函数f(x,y,z)≥0,并将它看做某物体的密度函数,通过计算该物体的质量引出下列各计算方法:
投影法(先一后二)
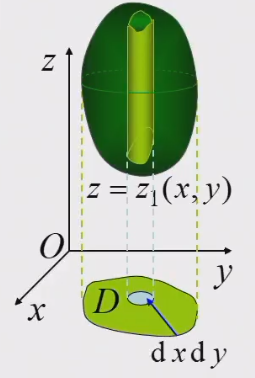
xy型区域Ω:{z1(x,y)≤z≤z2(x,y)(x,y)∈D
细长柱体微元的质量为
(∫z1(x,y)z2(x,y)f(x,y,z)dz)dxdy
该物体的质量为
∭Ωf(x,y,z)dv=∬D(∫z1(x,y)z2(x,y)f(x,y,z)dz)dxdy记作∬Ddxdy∫z1(x,y)z2(x,y)f(x,y,z)dz
截面法(先二后一)
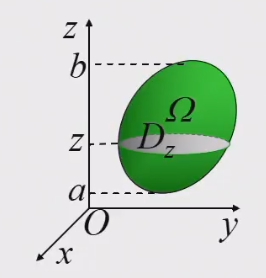
Ω:{(x,y)∈Dza≤z≤b
以D2为底,以dz为高的柱状薄片质量为
(∬Dzf(x,y,z)dxdy)dz
该物体的质量为
∭Ωf(x,y,z)dv=∫ab(∬Dzf(x,y,z)dxdy)dz记作∫abdz∬Dzf(x,y,z)dxdy
三次积分法
利用柱坐标计算三重积分
设M(x,y,z)∈R3,将x,y用极坐标ρ,θ代替,则(ρ,θ,z)就成为点M的柱坐标。
⎩⎪⎪⎨⎪⎪⎧x=ρcosθy=ρsinθz=z
坐标面分别为
ρ=常数⇒圆柱面θ=常数⇒半平面z=常数⇒平面
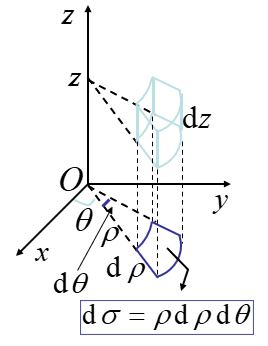
体积元素为dv=ρ dρ dθ dz
因此有∭ΩF(ρ,θ,z)ρ dρ dθ dz
利用球坐标计算三重积分
设M(x,y,z)∈R3,其柱坐标为(ρ,θ,z),令∣OM∣=r,∠zOM=φ,则(ρ,θ,φ)就称为点M的球坐标
⎩⎪⎨⎪⎧x=rsinφcosθy=rsinφsinθz=rcosφ
在球面坐标系中,体积元素为dv=r2sinφ dr dφ dθ
因此有∭ΩF(r,θ,φ)r2sinφ dr dφ dθ