信息安全原理与数学基础-代数结构、同态映射、形式语言

• 算术（arithmetic）：研究的是具体的运算法则和性质
• 代数（algebra）：算数的一般化，用字母等符号代替数

代数结构与抽象代数

代数结构（algebraic structure）：在一个对象集合上定义若干运算，并设定若干公理描述运算的性质，例如命题演算系统就是代数结构

抽象代数（abstract algebra）：抛弃代数结构中对象集合与运算的具体意义，研究运算的一般规律

运算

运算是$S^n$到$S$的一个函数，成为$n$元运算，常用$*$代表二元运算，$*(x,y)$常记作$x*y$。常用$\Delta$表示一元运算

运算的基本性质：

• 普遍性：$S$中的所有元素都可以参与运算
• $\forall x\forall y\exist z(x*y=z)$
• 单值性：相同的元素运算结果也相同且唯一
• $\forall x\forall y\forall x'\forall y'((x=x'\wedge y=y')\rightarrow(x*y=x'*y'))$
• 封闭性：任何元素参与运算的结果也是$S$中的元素
• $\forall x\forall y\exist z(x*y=z\rightarrow z\in S)$

二元运算的一般性质

• 结合律
• $\forall\mathrm{x}\forall\mathrm{y}\forall\mathrm{z}\left(\mathrm{x},\mathrm{y},\mathrm{z}\in\mathrm{S}\rightarrow\mathrm{x}*(\mathrm{y}*\mathrm{z})=(\mathrm{x}*\mathrm{y})*\mathrm{z}\right)$
• 交换律
• $\forall\mathrm{x}\forall\mathrm{y}\left(\mathrm{x},\mathrm{y}\in\mathrm{S}\rightarrow\mathrm{x}*\mathrm{y}=\mathrm{y}*\mathrm{x}\right)$​
• *运算对#运算满足分配分配律，如果：
• $\forall\mathrm{x}\forall\mathrm{y}\forall\mathrm{z}\left(\mathrm{x},\mathrm{y},\mathrm{z}\in\mathrm{S}\rightarrow\mathrm{x}*(\mathrm{y}\#\mathrm{z})=(\mathrm{x}*\mathrm{y})\#(\mathrm{x}*\mathrm{z})\right)$​

代数结构的定义

非空集合$S$，称作代数结构的载体

载体$S$上的若干运算

一组刻画载体上各运算的公理

例如：

• <N，+>是一个代数结构
• <$\rho(A),\cup,\cap,\sim$​>是一个代数结构

幺元（identity element）

代数结构$<S,*>$中的元素$e$，如果满足$\forall\mathrm{x}\left(\mathrm{x}*\mathrm{e}=\mathrm{e}*\mathrm{x}=\mathrm{x}\right)$，则称$e$为幺元。

如果仅满足$\forall x(x*e=x)$，称作右幺元

如果仅满足$\forall x(e*x=x)$​，称作左幺元

一般情况下，左右幺元可能是不同元素，也有可能有多个。如果存在幺元，那么幺元是唯一的并且同时是左右幺元。

零元（zero element）

代数结构$<S,*>$中的元素$o$，如果满足$\forall\mathrm{x}\left(\mathrm{x}*\mathrm{o}=\mathrm{o}*\mathrm{x}=\mathrm{o}\right)$，则称$o$为零元。

如果仅满足$\forall x(x*o=o)$，称作右零元

如果仅满足$\forall x(o*x=o)$​，称作左零元

一般情况下，左右零元可能是不同元素，也可能有多个。如果存在零元，那么零元是唯一的并且同时是左右零元

逆元（inverse element）

代数结构$<S,*>$中的幺元$e$，如果$x*y=e$，那么$x$称作$y$的左逆元，$y$称作$x$的右逆元。如果$x*y=y*x=e$，那么$x,y$互称逆元。$x$的逆元通常记作$x^{-1}$​。

多于一个元素的载体集上零元没有逆元。若$<S,*>$有幺元$e$，零元$o$，并且有$|S|>1$，那么$o$没有（左右）逆元。

在满足结合律的代数结构中，逆元是唯一的。

可约（cancelable）元素

$<S,*>$中元素$a$，如果对于任意$x,y\in S$​有

$\begin{aligned}&\mathrm{a*x=a*y\models x=y\text{(左可约)}}\\&\mathrm{x*a=y*a\models x=y\text{(右可约)}}\end{aligned}$​

称$a$是可约的。

在满足交换律的代数结构中，有逆元的元素是可约的。

同构

如$<\{A,\emptyset\},\cup>,<\{1,0\},\vee>$​中，除了符号外，结构完全相同，可以通过符号的变换（一一映射）相互转化。则我们称这两个代数结构是同构的

• 同类型的代数结构：$|S|=|S'|$且运算的元数相同
• 同构的代数结构：存在$S\rightarrow S'$的一一映射$h$。$S$中运算的像等于运算数像在$S'$的运算结果$h(x*y)=h(x)\circ h(y)$。其中$*$是$S$中的运算，而$\circ$是$S'$上的运算

同态映射（homomorphism）

代数结构之间，更为一般性的相似关系。

对于代数结构$<S,\Delta,#> $和 $<S',\Delta',\#'>$, 如果有函数 $h:S\to S^{\prime}$, 对$S$中任意元素$a,b$

$$h(\Delta(a))=\Delta^{\prime}\left(h(a)\right),h(a\#b)=h(a)\#^{\prime}h(b)$$

函数$h$就称作代数结构$S$到$S'$​的同态映射。

• 如果$h$是单射函数，称作单一同态
• 如果$h$是满射函数，称作满同态
• 如果$h$是双射函数，称作同构映射(isomorphism)

满同态映射

$<\Sigma^*,||>$和$<N,+>$之间（||代表连接）存在满同态映射$len(w)=|w|$

$len(u||v)=|u||v|=|u|+|v|=len(u)+len(v)$

表明了字符串连接和自然数加法之间的相似性，可以用连接操作来模拟加法运算

同余关系

代数结构$<S,\Delta,*>$中，$S$上的一个等价关系$\sim$，如果满足$a\sim b$蕴含$\Delta a\sim \Delta b$，则称$\sim$是$S$上关于一元运算$\Delta$的同余关系。如果满足$a\sim b,c\sim d$蕴含$a*c\sim b*d$，则称$\sim$是$S$上关于二元运算$*$的同余关系。

等价类$[x]_\sim$称为同余类

代数结构的类型

若$<S,*>$满足结合律，则被称为半群（semigroup）

若半群含有幺元，则称为独异点（monoid）

若独异点每个元素都有逆元且没有零元，则称之为群（group）

若群满足交换律，则称为阿贝尔群（Abel group)。

环（ring）：

• $<R,+,*>$，有两个二元运算
• $<R,+>$是阿贝尔群
• $<R,*>$​是半群
• $*$对$+$可分配：$a*(b+c)=a*b+a*c,(b+c)*a=b*a+c*a$

域（field）：

• $<F,+,*>$，有两个二元运算
• $<F,+,*>$是环
• $<F-\{o\},*>$​为阿贝尔群

$S=\{0,1,2,3\}$，+解释为$+\ mod\ 4$，$*$解释为$*\ mod\ 4$​

则$<S,+,*>$是环

而$S=\{0,1,2,3,4\}$，+解释为$+\ mod\ 5$，$*$解释为$*\ mod\ 5$​

则$<S,+,*>$是域

形式语言

自然语言

以呼吸器官发声为基础来传递信息的符号系统，是大脑思维的符号化。

自然语言：自然地随着文化演化的语言

人工语言

以特定的目的与用途，人为创造的语言

国际辅助语言：世界语

数学语言、计算机语言

数学符号、逻辑语言

程序设计语言

语音（Phonetics）：发音的体系

发音包括：音素、音节、语调

国际音标建立了标准的发音体系

语形（Morphology）：书写的格式和规范

拼音文字：以发音为基础构字，一维表意串

genshin impact……

象形文字：以二维表意图形为基础构字

原、神、启、动……

句法（Syntax）：规定句子组成的规则

语句的符号和意义都不可以穷举。

主谓宾定状补：小明正在树下读书

但是语法对于意义无能为力：书一下午读了3本小明

语义（Semantics）：语句的含义

从符号语言还原思维：思维->语言->传递->语言->思维

共同理解和保持语义是人类交流的基础

语言交流存在语义损耗，因而有时说“一图胜千言”

如何形式化表达语义是目前研究的热点难题

语用（Pragmatics）：使用环境和功能

不同的上下文环境中语句的应用，对语义的影响

语用的研究是自然语言处理NLP的重要内容

语言的定义

Chomsky：按照一定规律构成句子和符号串的有限或者无限集合

穷举法：只适合句子数目有限的语言

语法描述：通过有限的替换规则，生成语言中合格的句子

自动机：对输入的句子进行检验，区别哪些是语言中的句子，哪些不是语言中的句子

设$V$是有限集合，其中元素称为"字符"，由$V$中字符相连而成的有限序列成为“字符串”。不包含任何字符的串称为空串，记作$\varepsilon$，字符串所包含的字符个数称为长度，记作$|s|$，$|\varepsilon|=0$。包括空串的$V$上的字符串全体记作$V^*$。

字符串连接：$s=ab,t=cd,st=abcd$

字符串n次幂：$s$自身连接n次，$s^0=\varepsilon$

乘积：$AB=\{st|s\in A\wedge t\in B\}$

幂运算：$A^0=\{\varepsilon \},A^n=A^{n-1}A=AA^{n-1}$

闭包：$A^*=A^0\cup A^1\cup A^2\cup...$

正闭包：$A^+=A^1\cup A^2\cup A^3\cup ...=A^*-\{\varepsilon\}$

正则表达式

RE1：$\varepsilon$是正则式，对应正则集$\{\varepsilon\}$

RE2：x$\in V$​，x是正则表达式，对应正则集{x}

RE3：如果a、b是正则表达式，则ab是正则式，对应正则集AB

RE4：如果a、b是正则式，则（a|b）是正则式，对应正则式A$\cup$B

RE5：如果a是正则式，则（a）*是正则式，对应正则集A*

例V={a,b}

• ab*b描述了{ab,abb,abbb…}
• ab*描述了{a,ab,abb,abbb…}
• a*b*描述了{$\varepsilon$,a,b,aab,abb…}
• (ab)*描述了{$\varepsilon$,ab,abab,ababab…}

短语结构语法

短语结构语法是一个四元组G=<V,S,$\mathrm{v}_0$,$\vdash$​>

V是字符集。S$\subseteq$​V，称做终结符，N=V-S称作非终结符。$\vdash$称作产生式关系，由w$\vdash$​w’的这样的产生式构成，表示w可以替换成w‘，分别称为左部和右部。$\mathrm{v}_0\in \mathrm{N}$，称为初始符，是替换的起点。

V*上的二元关系：

直接导出关系（x$\rightarrow$y）定义为x=awb,y=aw’b，且w$\vdash$w’是产生式，a,b$\in$​V*

$\rightarrow$关系的传递闭包$\rightarrow^\infin$，w$\in$S*是语法正确的句子当且仅当$\mathrm{v}_0\rightarrow^\infin \mathrm{w}$

利用语法G产生的所有的正确构造的句子的集合称作为G的语言，记作L(G)

导出树

用多元有向树表示语言导出过程

• 起始符$\mathrm{v}_0$作为树根
• 每个子树的树根是某个生成式的左部
• 子节点分别是生产式右部包含的符号
• 适合所有产生式的左部仅有一个非终结符情形

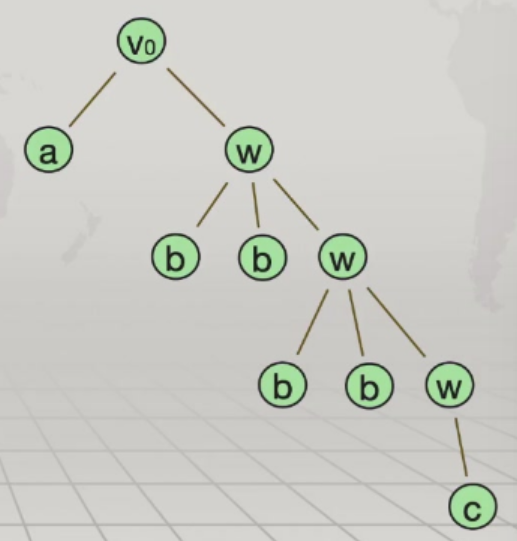
例如V={$\mathrm{v}_0$,w,a,b,c},S={a,b,c}

产生式：$\mathrm{v}_0\vdash$aw；w$\vdash$bbw；w$\vdash$c

L(G)$\subseteq$​S*

可以对应正则表达式a(bb)*c

再例如V={$\mathrm{v}_0$,w,a,b,c},S={a,b,c}

产生式：$\mathrm{v}_0\vdash\mathrm{av}_0\mathrm{b}$；$\mathrm{v}_0$b$\vdash$bw；abc$\vdash$c

可以分析，第一个产生式产生形如$a^nv_0b^n$这样的串，第二个产生式结果形如$v^mabwb^m$，第三个产生式消除非终结符，结果L(G)形如$a^mcb^m$​。L(G)不能用正则表达式表达，可见语言之间有某种类型上的差异

语法分类

• 若对产生式没有任何约束，称作0型语言，无限制语法，产生递归可枚举语言，被图灵机识别
• 如果所有产生式形如aAb$\vdash$​acb，A是非终结符，a,b,c是任意串，但c不能为空串，称作1型语言。是上下文相关语法，产生上下文相关语言，被线性有界自动机识别。
• 如果所有产生式左部是一个非终结符，形如A$\vdash$​b(b是任意串)，称作2型语言，是一种上下文无关语法。产生上下文无关语言，被下推自动机识别。为大多数程序设计语言的语法提供理论基础
• 如果所有产生式左部是一个非终结符，右部最多一个非终结符，且只能在最右端，称作3型语言，是正则语法。产生正则语言，被有限状态自动机识别

BNF(Backus-Naur Form)范式

1960年提出的用于描述ALGO60语言。形式简单，仅包含三个符号："::=“定义为，”|“或，”<>"用于区分非终结符。

BNF可以表示2、3型语法。BNF的产生式左部仅有一个非终结符，相同左部的产生式和并用"|“隔开，非终结符用”<>"标记

正则集合与正则语法

S是有限集合，L$\subseteq$S*，则L是正则集合，当且仅当：对某个正则语法G，有L=L(G)

我们可以从正则语法G构造对应正则集合的正则表达式，将G的语法组合为一个大图，其中仅包含$\mathrm{v}_0$​和终结符，称作主导图（master diagram），语法图中终结符对应正则表达式中的终结符。

句子识别

给定一个字符串，判定是否属于给定语法G的语言L(G)。对于正则语言和正则语法，可以通过一个识别机器来判定。

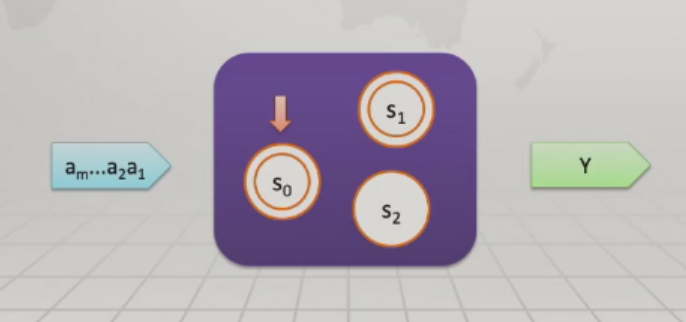
机器

一个系统，接受输入，改变自身的状态，产生输出。状态指为了完成机器的任务而对输入序列进行的一种临时归类。机器状态会发生多次改变，最终停止在某个状态，并产生输出。若对于所有的输入，机器状态的数目有限，则被称为有限状态机。

有限状态机是一个五元组M(A,S,Y,$\mathrm{s}_0$,F)

• A：输入字符的字母表
• S：机器的有限状态集合
• Y$\subseteq$S：被称为”接受“的一些状态
• $\mathrm{s}_0\in S$：初始状态
• F:S$\times$A$\rightarrow$​S：状态转移函数

泵引理

长度超过状态数目的接受串w，都可以表示成w=xyz形式，而x$\mathrm{y}^m$z都会被M接受

带输出的状态机

在有限状态机M(A,S,Y,$\mathrm{s}_0$,F)的基础上，去掉接收状态集合Y，增加输出字符的有限集合Z，输出函数G:S$\times$A$\rightarrow$Z。在状态转移的同时，输出一个字符。可以通过带输出的有限状态机实现二进制加法