大物-相对论II

• 狭义相对论质速关系、动力学方程

• 质能关系、能动关系

• 广义相对论

狭义相对论质速关系、动力学方程

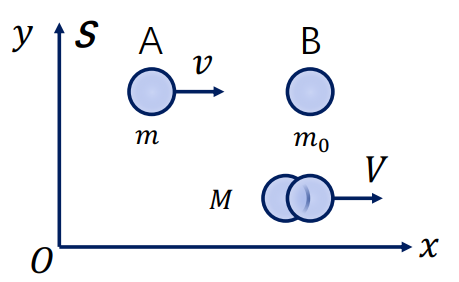
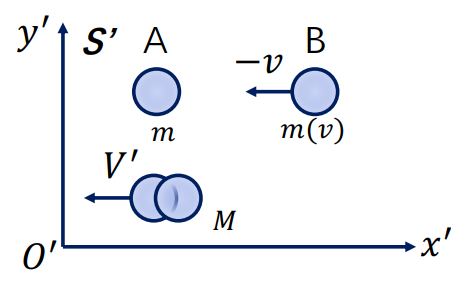
在如图所示的运动当中，若按照原先定义动量为质量乘上速度，则有$m_0v=2m_0V$，从而$V=v/2$。但在以相对于S以$v$速度运动的参考系S’的情况下，有$V'=\frac{V-v}{1-Vv/c^2}=-\frac{v}{2}\frac{1}{1-v^2/2c^2}$，显然不满足$-m_0v=2m_0V'$​。

动量$\overrightarrow{p}$与速度$\overrightarrow{v}$不再成正比。因此，为了让动量定理继续成立，我们把对正比关系的偏离归结到比例系数m内。设：$m=m(v)$。有质量守恒$m(v)+m_0=M(V)$，动量守恒$m(v)v=M(V)V\Rightarrow\frac{M(V)}{m(v)}=\frac{v}{V}$

$$\Rightarrow m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}$$

其中$m_0$为静止质量，$m$​为运动质量。因此我们也可以得出结论：当物体速度趋向于光速时，质量趋向于无穷大。并且光子没有静止质量。

$$\text{相对论动能：}\overrightarrow{p}=m\overrightarrow{v}=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\overrightarrow{v}$$

$$\text{动力学方程：}\overrightarrow{F}=\frac{d\overrightarrow{p}}{dt}=\frac{d}{dt}(\frac{m_0\overrightarrow{v}}{\sqrt{1-\frac{v^2}{c^2}}})$$

在这道例题中，我们有

$$\tag{1}mv=MV$$

$$\tag{2}m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}$$

$$\tag{3}m_0+m=M$$

$$\Rightarrow M=m_0+m_0/0.6=\frac{8}{3}m_0\\ \Rightarrow V=0.5c\\ \Rightarrow M_0=\frac{4\sqrt{3}}{3}m_0$$

质能关系、能动关系

由动能定律，外力做功等于物体动能的增量：

$$dE_k=\vec{F}\cdot d\vec{r}=\frac{d\vec{p}}{dt}\cdot d\vec{r}=\vec{v}\cdot d\vec{p}=\vec{v}\cdot(\vec{v}dm+md\vec{v})$$

对$dm$微分有$dm=\frac{m_0vdv}{c^2(1-v^2/c^2)^{3/2}}\Rightarrow dm(c^2-v^2)=mvdv$

代入原式，我们可以得到

$$dE_k=c^2dm$$

$$\int_0^{E_k}dE_k=\int_{m_0}^{m}c^2dm \Rightarrow E_k=mc^2-m_0c^2$$

同时有$v\ll c \Rightarrow E_k\approx \frac{1}{2}m_0v^2$

我们得到关于动能的表达式$E_k=mc^2-m_0c^2 \Rightarrow E=E_k+E_0$。其中$E$就是总能量，而$E_0$就是静能量。

根据已经获得的关系式，我们可以的出能动关系$E^2=p^2c^2+E_0^2$。

（1）由动能定理

$$W=\vec{F}d=E_{K2}-E_{K1}=\frac{m_0c^2}{\sqrt{1-(\upsilon_2^2/c^2)}}-\frac{m_0c^2}{\sqrt{1-(\upsilon_1^2/c^2)}}\\ \Rightarrow\vec{F}=-10^{-10}N$$

（2）由动量定理

$$\vec{F}\Delta t=m_2v_2-m_1v_1\\ \Rightarrow \Delta t=\frac{1}{3}\times 10^{-8}s$$

广义相对论

广义相对论的两条基本假设：

• 等效原理： 引力与加速系中的惯性力局部等效。

• 广义协变原理： 物理规律在任何参照系（包括非惯性系）中形式相同。

根据这两个基本假设，可以推出：引力场中时空发生弯曲

依据广义相对论原理，我们观察到了诸多验证广义相对论的现象，如引力红移（引力场中时间膨胀将导致原子发光频率降低，谱线红移），光线偏转（由于时空弯曲，光线在引力场中发生偏转）。